có:
\(\sqrt{n+1}-\sqrt{n}\)
\(=\dfrac{\left(\sqrt{n+1}-\sqrt{n}\right)\left(\sqrt{n+1}+\sqrt{n}\right)}{\sqrt{n+1}+\sqrt{n}}\)
\(=\dfrac{n+1-n}{\sqrt{n+1}+\sqrt{n}}=\dfrac{1}{\sqrt{n+1}+\sqrt{n}}\)
Vì \(2\sqrt{n}< \sqrt{n+1}+\sqrt{n}< 2\sqrt{n+1}\)
\(\Rightarrow\dfrac{1}{2\sqrt{n}}>\dfrac{1}{\sqrt{n+1}+\sqrt{n}}>\dfrac{1}{2\sqrt{n+1}}\)
Vậy: \(\dfrac{1}{2\sqrt{n+1}}< \sqrt{n+1}-\sqrt{n}< \dfrac{1}{2\sqrt{n}}\)

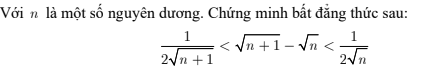 các bạn giúp mình đc ko ạ
các bạn giúp mình đc ko ạ