Câu 14:
Thay x=1 và y=1 vào hệ, ta được:
\(\left\{{}\begin{matrix}1+1\left(1-a\right)=-2\\b+3=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}1+1-a=-2\\b=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2-a=-2\\b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=4\\b=4\end{matrix}\right.\)
\(T=a^2-2b=4^2-2\cdot4=8\)
=>Chọn B
Câu 15:
Thay x=-1 và y=5 vào hệ, ta được:
\(\left\{{}\begin{matrix}\left(2a+1\right)\cdot\left(-1\right)-5=4\\-1+5\left(b-3\right)+11=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2a-1-5=4\\5\left(b-3\right)=-10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-2a=4+5+1=10\\b-3=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-5\\b=1\end{matrix}\right.\)
T=a+3b=-5+3=-2
=>Chọn A
Câu 16:
\(\left\{{}\begin{matrix}2\left(x-1\right)+y=7\\x-3\left(y+1\right)=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+y=9\\x-3y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}6x+3y=27\\x-3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7x=28\\2x+y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=1\end{matrix}\right.\)
mx-2y=3m+8
=>4m-2=3m+8
=>m=10
=>Chọn D
Câu 17:
Để hệ vô số nghiệm thì \(\dfrac{4}{2}=\dfrac{m^2}{m}=\dfrac{3m-6}{-3}\)
=>\(m=-m+2=2\)
=>m=2; -m+2=2
=>\(m\in\varnothing\)
=>Chọn D
Câu 18:
Để hệ có nghiệm duy nhất thì \(\dfrac{2}{5}\ne\dfrac{-3a}{3}\)
=>\(-a\ne\dfrac{2}{5}\)
=>\(a\ne-\dfrac{2}{5}\)
=>Chọn A
Câu 19:
a: Vì \(\dfrac{3}{-6}=\dfrac{-2}{4}=\dfrac{4}{-8}=-\dfrac{1}{2}\)
nên hệ có vô số nghiệm
b:Vì \(\dfrac{-2}{3}\ne\dfrac{1}{-2}\)
nên hệ có 1 nghiệm duy nhất
c: Vì \(\dfrac{\sqrt{2}}{3\sqrt{2}}=\dfrac{-2}{-6}\ne\dfrac{3}{-5}\)
nên hệ không có nghiệm
d: Vì \(\dfrac{3}{2}\ne\dfrac{-0}{-5}\)
nên hệ có 1 nghiệm duy nhất












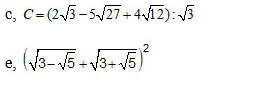
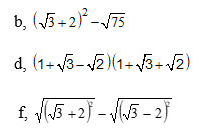 các bạn giải hộ mik mấy câu này vs mik đag cần gấp
các bạn giải hộ mik mấy câu này vs mik đag cần gấp












 ).
).
















