a: ĐKXĐ: x>=1
\(\sqrt{4x-4}+\sqrt{9x-9}=25\)
=>\(2\sqrt{x-1}+3\sqrt{x-1}=25\)
=>\(5\sqrt{x-1}=25\)
=>x-1=25
=>x=26(nhận)
b: \(\sqrt{4x^2-4x+1}=x-2\)
=>\(\sqrt{\left(2x-1\right)^2}=x-2\)
=>\(\left\{{}\begin{matrix}x>=2\\\left(2x-1\right)^2=\left(x-2\right)^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=2\\\left(2x-1-x+2\right)\left(2x-1+x-2\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=2\\\left(x+1\right)\left(3x-3\right)=0\end{matrix}\right.\Leftrightarrow x\in\varnothing\)
c: \(\sqrt{x^2+4x+4}=2x-3\)
=>\(\sqrt{\left(x+2\right)^2}=2x-3\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{3}{2}\\\left(2x-3\right)^2=\left(x+2\right)^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{3}{2}\\\left(2x-3-x-2\right)\left(2x-3+x+2\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{3}{2}\\\left(x-5\right)\left(3x-1\right)=0\end{matrix}\right.\Leftrightarrow x=5\)
d: ĐKXĐ: 8-x>=0
=>x<=8
\(\sqrt{8-x}=x-2\)
=>\(\left\{{}\begin{matrix}x-2>=0\\\left(x-2\right)^2=8-x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2< =x< =8\\x^2-4x+4+x-8=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2< =x< =8\\x^2-3x-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2< =x< =8\\\left(x-4\right)\left(x+1\right)=0\end{matrix}\right.\)
=>x=4
e: ĐKXĐ: x>=3
\(\sqrt{x-3}>2\)
=>x-3>4
=>x>7
f: ĐKXĐ: x>=0
\(\dfrac{4}{\sqrt{x}+1}>1\)
=>\(\dfrac{4}{\sqrt{x}+1}-1>0\)
=>\(\dfrac{4-\sqrt{x}-1}{\sqrt{x}+1}>0\)
=>\(3-\sqrt{x}>0\)
=>\(\sqrt{x}< 3\)
=>0<=x<9


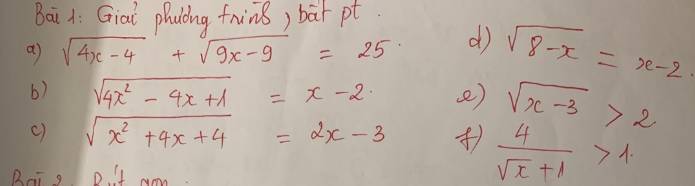




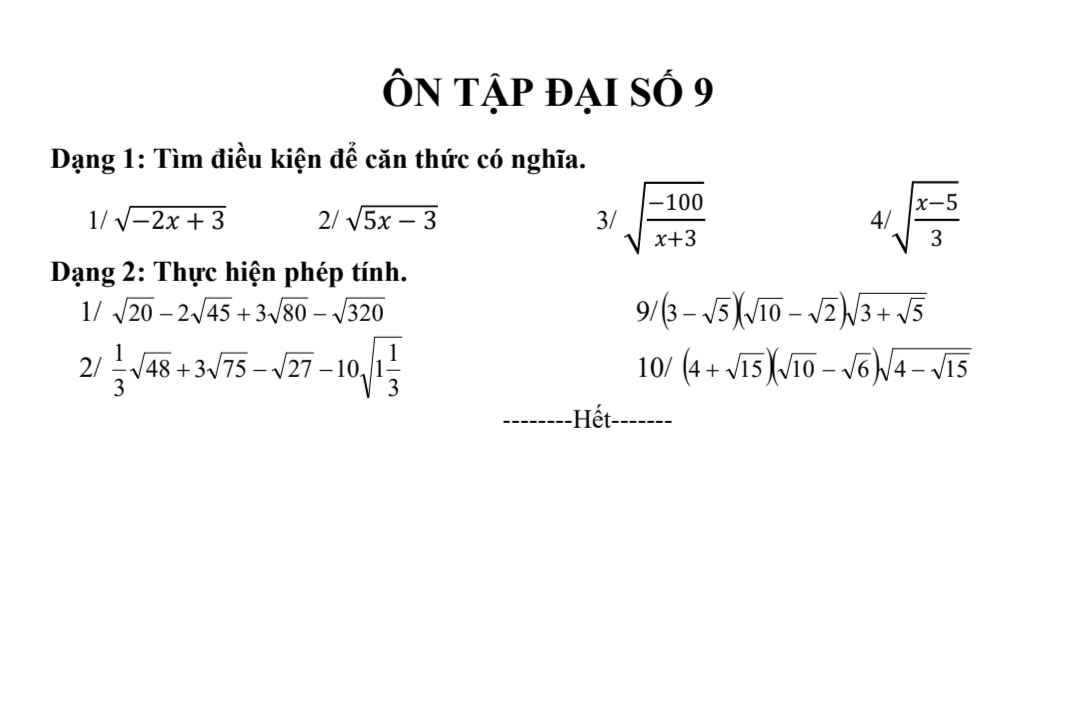



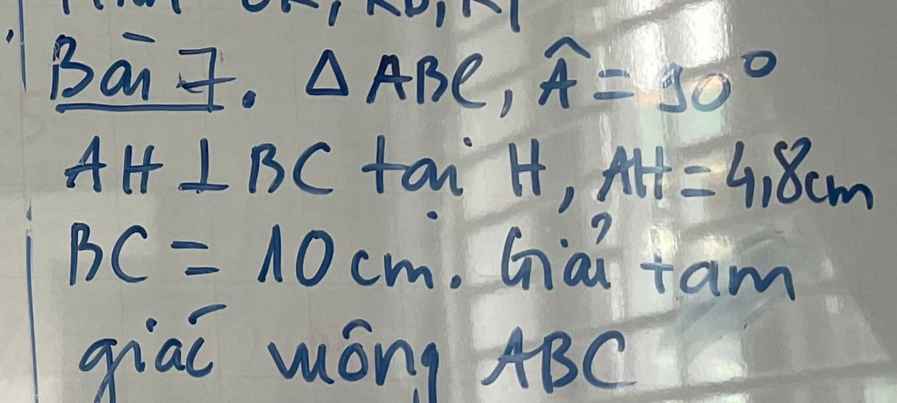

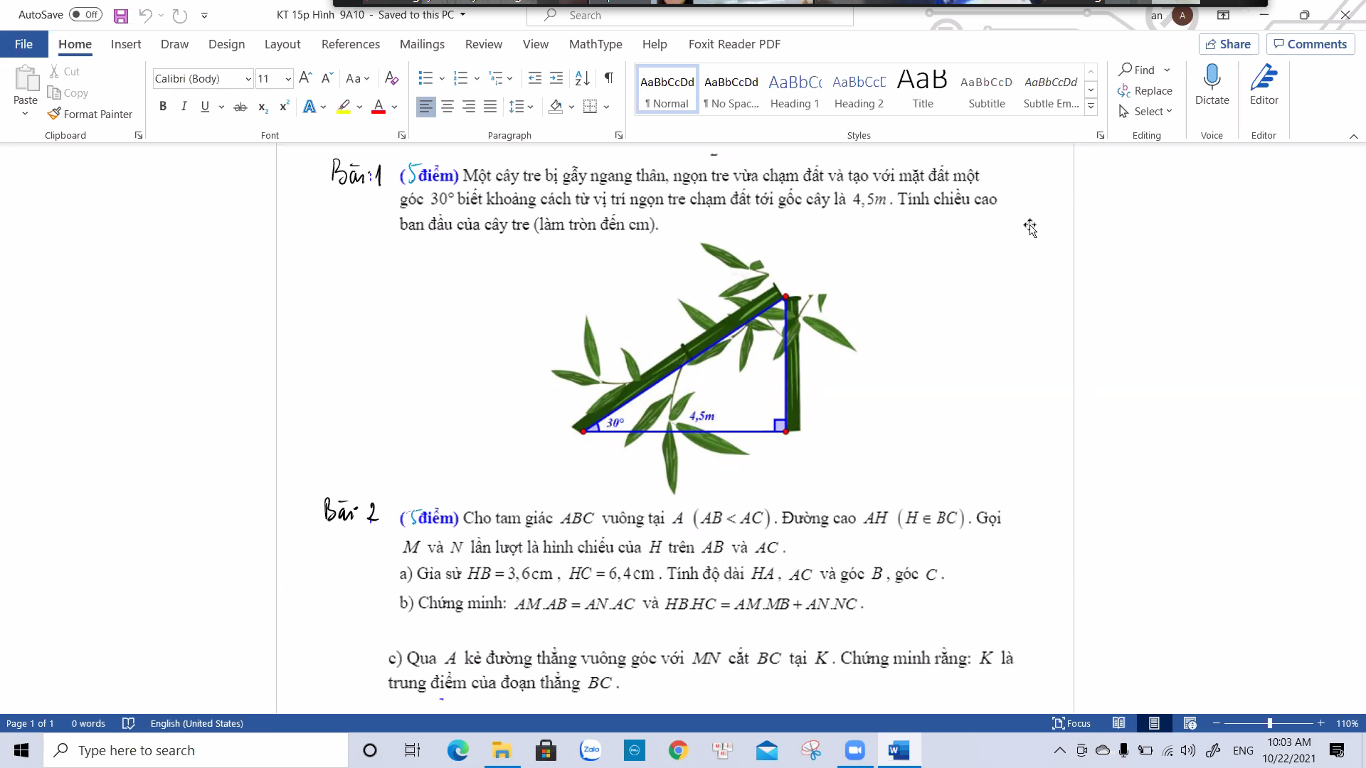




 giúp em với ạ, cần gấp ạ TvT
giúp em với ạ, cần gấp ạ TvT


