Question

BT: Cho tam giác ABC vuông tại A, đường cao AH, gọi D,E lần lượt là chân các đường vuông góc kẻ từ H đến AB và AC a) Chứng minh AH=DE b) Gọi I là trung điểm của HB, K là trung điểm của HC. Chứng minh DI song song với EK

Answer 1

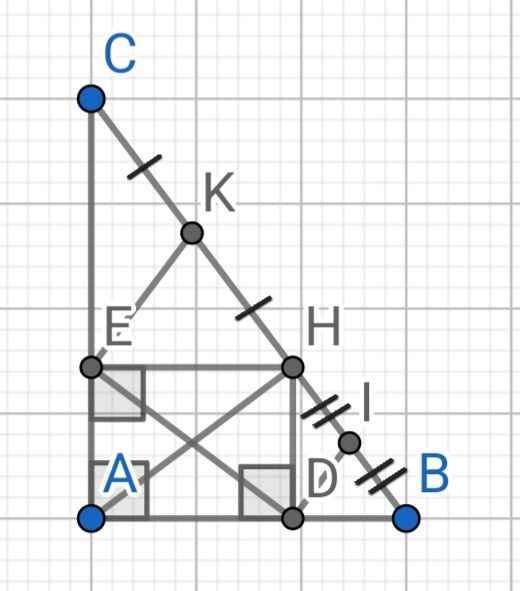
   a) Tứ giác ADHE có:

∠AEH = ∠ADH = ∠HAE = 90⁰ (gt)

⇒ ADHE là hình chữ nhật

⇒ AH = DE

b) BHD vuông tại D

I là trung điểm của HB (gt)

⇒ ID = IH = BH : 2

⇒ ∆IDH cân tại I

⇒ ∠IDH = ∠IHD

⇒ ∠HID = 180⁰ - (∠IDH + ∠IHD)

= 180⁰ - 2∠IHD (1)

∆CEH vuông tại E

K là trung điểm HC (gt)

⇒ KE = KC = HC : 2

⇒ ∆KEC cân tại K

⇒ ∠KEC = ∠KCE

⇒ ∠CKE = 180⁰ - (∠KEC + ∠KCE)

= 180⁰ - 2∠KEC (2)

Do HD ⊥ AB (gt)

AC ⊥ AB (gt)

⇒ HD // AC

⇒ ∠IHD = ∠KCE (đồng vị)

⇒ 2∠IHD = 2∠KCE (3)

Từ (1), (2) và (3) ⇒ ∠CKE = ∠HID

Mà ∠CKE và ∠HID là hai góc đồng vị

⇒ DI // KE