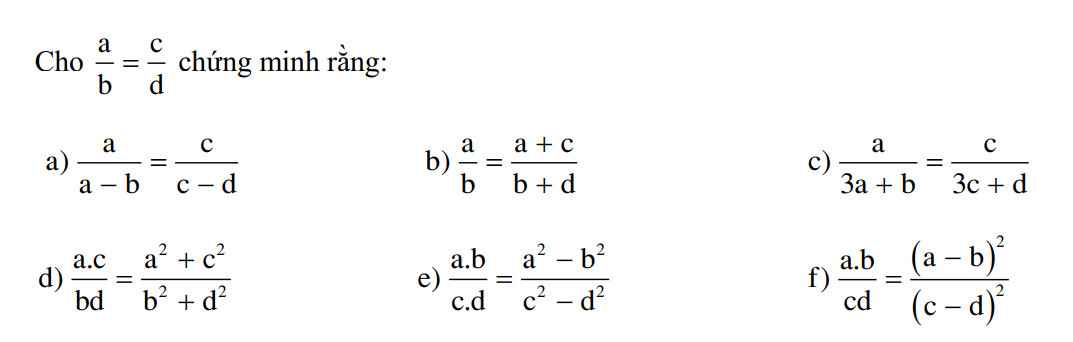\(a,\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a-b}{c-d}\Rightarrow\dfrac{a}{a-b}=\dfrac{c}{c-d}\\ b,\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{a+c}{b+d}\\ c,\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{3a+b}{3c+d}\Rightarrow\dfrac{a}{3a+b}=\dfrac{c}{3c+d}\\ d,\text{Đặt }\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\\ \Rightarrow\dfrac{ac}{bd}=\dfrac{bk\cdot dk}{bd}=k^2\left(1\right)\\ \dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a^2}{b^2}=\dfrac{c^2}{d^2}=\dfrac{a^2+c^2}{b^2+d^2}=\left(\dfrac{a}{b}\right)^2=k^2\left(2\right)\\ \left(1\right)\left(2\right)\Rightarrow\dfrac{ac}{bd}=\dfrac{a^2+c^2}{b^2+d^2}\)
\(e,\text{Đặt }\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\\ \Rightarrow\dfrac{ab}{cd}=\dfrac{bk\cdot b}{dk\cdot d}=\dfrac{b^2}{d^2}\left(1\right)\\ \dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}\Rightarrow\dfrac{a^2}{c^2}=\dfrac{b^2}{d^2}=\dfrac{a^2-b^2}{c^2-d^2}\left(2\right)\\ \left(1\right)\left(2\right)\Rightarrow\dfrac{ab}{cd}=\dfrac{a^2-b^2}{c^2-d^2}\\ f,\text{Đặt }\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\\ \Rightarrow\dfrac{ab}{cd}=\dfrac{bk\cdot b}{dk\cdot d}=\dfrac{b^2}{d^2}=\left(\dfrac{b}{d}\right)^2\left(1\right)\\ \dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a-b}{c-d}\Rightarrow\left(\dfrac{b}{d}\right)^2=\left(\dfrac{a-b}{c-d}\right)^2=\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}\left(2\right)\\ \left(1\right)\left(2\right)\RightarrowĐpcm\)