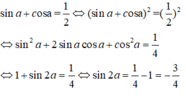Các câu hỏi tương tự
Cho tam giác ABC có góc A tù. Cho các biểu thức sau: (1) M sin A + sin B + sin C (2) N cosA. cosB. cosC (3)
P
cos
A
2
.
sin
B
2
.
c
o
t
C
2
(4) Q cotA.tan B.tan C Số các b...
Đọc tiếp
Cho tam giác ABC có góc A tù. Cho các biểu thức sau:
(1) M = sin A + sin B + sin C
(2) N = cosA. cosB. cosC
(3) P = cos A 2 . sin B 2 . c o t C 2
(4) Q = cotA.tan B.tan C
Số các biểu thức mang giá trị dương là:
A. 1
B. 2
C. 3
D. 4
Cho A, B, C là 3 góc trong tam giác. Chứng minh rằng:1, sin A + sin B - sin C 4sindfrac{A}{2} sin dfrac{B}{2}sin dfrac{C}{2}2, dfrac{sinA+sinB-sinC}{cosA+cosB-cosC+1}tandfrac{A}{2}tandfrac{B}{2}tandfrac{C}{2} (ΔABC nhọn)3, dfrac{cosA+cosB+cosC+3}{sinA+sinB+sinC}tandfrac{A}{2}+tandfrac{B}{2}+tandfrac{C}{2}GIÚP MÌNH VỚI!!!
Đọc tiếp
Cho A, B, C là 3 góc trong tam giác. Chứng minh rằng:
1, sin A + sin B - sin C = 4sin\(\dfrac{A}{2}\) sin \(\dfrac{B}{2}\)sin \(\dfrac{C}{2}\)
2, \(\dfrac{sinA+sinB-sinC}{cosA+cosB-cosC+1}=tan\dfrac{A}{2}tan\dfrac{B}{2}tan\dfrac{C}{2}\) (ΔABC nhọn)
3, \(\dfrac{cosA+cosB+cosC+3}{sinA+sinB+sinC}=tan\dfrac{A}{2}+tan\dfrac{B}{2}+tan\dfrac{C}{2}\)
GIÚP MÌNH VỚI!!!
Biết sina + cosa = 2 /2. Giá trị sin2a là
A. 2 2 /3 B. -2/3
C. -1/2 D. 1/2
Giải các pt
a) \(\sqrt{2}\sin\left(2x+\dfrac{\pi}{4}\right)=3\sin x+\cos x+2\)
b) \(\dfrac{\left(2-\sqrt{3}\right)\cos x-2\sin^2\left(\dfrac{x}{2}-\dfrac{\pi}{4}\right)}{2\cos x-1}=1\)
c) \(2\sqrt{2}\cos\left(\dfrac{5\pi}{12}-x\right)\sin x=1\)
[1] Cho hai tập hợp A = { 1; 2; 3; 4; 5 }; B = { 3; 4; 5 }. Biết B \(\subset A\), xác định tập hợp T = \(C_AB\)
A. T = { 1; 2; 3 } B. T = { 3; 4: 5 } C. T = { 1; 2 } D. T = { 1; 2; 3; 4; 5 }
biết cot a =1/2. giá trị biểu thức A = \(\dfrac{4\sin\alpha+5\cos\alpha}{2\sin\alpha-3\cos\alpha}\) bằng bao nhiêu?
Biết cotα=1/2. Gía trị biểu thức A=\(\dfrac{4\sin\alpha+5\cos\alpha}{2\sin\alpha-3\cos\alpha}\) bằng bao nhiêu?
Biết cotα=1/2. Gía trị biểu thức A=\(\dfrac{4\sin\alpha+5\cos\alpha}{2\sin\alpha-3\cos\alpha}\) bằng bao nhiêu?
Bài 1: Tìm a, b biết đường thẳng y ax + ba) Đi qua hai điểm A (-4; 2) và B (-1; 3)b) Đi qua điểm C (4; -1) và song song đường thẳng: y 2x + 4c) Đi qua điểm D (-2; 3) và vuông góc đường thẳng: y -3x + 1Bài 2: Tìm a, b, c biết parabol y ax2 + bx + c đi qua A (1; -4) và có đỉnh I (3; -8)Bài 3: Xét tính chẵn, lẻ của các hàm số sau:a) y x4 + 6x2 + 1b) y 2x + 3c) y sqrt{7-x}-sqrt{7-x}
Đọc tiếp
Bài 1: Tìm a, b biết đường thẳng y = ax + b
a) Đi qua hai điểm A (-4; 2) và B (-1; 3)
b) Đi qua điểm C (4; -1) và song song đường thẳng: y = 2x + 4
c) Đi qua điểm D (-2; 3) và vuông góc đường thẳng: y = -3x + 1
Bài 2: Tìm a, b, c biết parabol y = ax2 + bx + c đi qua A (1; -4) và có đỉnh I (3; -8)
Bài 3: Xét tính chẵn, lẻ của các hàm số sau:
a) y = x4 + 6x2 + 1
b) y = 2x + 3
c) y = \(\sqrt{7-x}-\sqrt{7-x}\)