Các câu hỏi tương tự
Tập hợp tất cả các điểm trong mặt phẳng toạ độ Oxy biểu diễn số phức z thoả mãn
z
-
1
+
2
i
z
+
3
là đường thẳng có phương trình
Đọc tiếp
Tập hợp tất cả các điểm trong mặt phẳng toạ độ Oxy biểu diễn số phức z thoả mãn z - 1 + 2 i = z + 3 là đường thẳng có phương trình
![]()
![]()
![]()
![]()
Xét các số phức z thoả mãn
z
¯
+
2
i
z
+
3
là số thuần ảo. Trên mặt phẳng toạ độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng
A
.
13
B
.
11
C....
Đọc tiếp
Xét các số phức z thoả mãn z ¯ + 2 i z + 3 là số thuần ảo. Trên mặt phẳng toạ độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng
A . 13
B . 11
C. 11 2
D. 13 2
Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn số phức z thỏa mãn
1
≤
z
≤
2
là một hình phẳng tích bằng
Đọc tiếp
Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn số phức z thỏa mãn 1 ≤ z ≤ 2 là một hình phẳng tích bằng
![]()
![]()
![]()
![]()
Gọi H là hình biểu diễn tập hợp các số phức z trong mặt phẳng tọa độ Oxy sao cho
2
z
-
z
≤
3
và số phức z có phần ảo không âm. Tính diện tích hình H A. 3π B.
3
π
4
C.
3...
Đọc tiếp
Gọi H là hình biểu diễn tập hợp các số phức z trong mặt phẳng tọa độ Oxy sao cho 2 z - z ≤ 3 và số phức z có phần ảo không âm. Tính diện tích hình H
A. 3π
B. 3 π 4
C. 3 π 2
D. 6π
Xét các số phức z thỏa mãn (
z
¯
+i)(z+2) là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng A. 1 B.
5
4
C.
5
2
D.
3
2
Đọc tiếp
Xét các số phức z thỏa mãn ( z ¯ +i)(z+2) là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả
các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng
A. 1
B. 5 4
C. 5 2
D. 3 2
Gọi (H) là hình biểu diễn tập hợp các số phức z trong mặt phẳng tọa độ Oxy để số phức z có phần thực không âm. Tính diện tích hình (H).
Đọc tiếp
Gọi (H) là hình biểu diễn tập hợp các số phức z trong mặt phẳng tọa độ Oxy để ![]() số phức z có phần thực không âm. Tính diện tích hình (H).
số phức z có phần thực không âm. Tính diện tích hình (H).
![]()
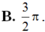
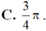
![]()
Tập hợp tất cả các điểm biểu diễn số phức z thoả mãn
z
2
+
z
+
z
¯
0
là một đường tròn, diện tích giới hạn bởi đường tròn đó bằng
Đọc tiếp
Tập hợp tất cả các điểm biểu diễn số phức z thoả mãn z 2 + z + z ¯ = 0 là một đường tròn, diện tích giới hạn bởi đường tròn đó bằng
![]()
![]()
![]()
![]()
Xét các số phức z thỏa mãn điều kiện |z-3+2i|5. Trong mặt phẳng tọa độ Oxy, tập hợp của điểm biểu diễn số phức z là A.Đường tròn tâmI(3;-2),bán kính R5 B.Đường tròn tâm I(-2;1), bán kính R5 C.Đường tròn tâm I(4;-3),bán kính R5. D. Đường tròn tâm I(-4;3), bán kính R5
Đọc tiếp
Xét các số phức z thỏa mãn điều kiện |z-3+2i|=5. Trong mặt phẳng tọa độ Oxy, tập hợp của điểm biểu diễn số phức z là
A.Đường tròn tâmI(3;-2),bán kính R=5
B.Đường tròn tâm I(-2;1), bán kính R=5
C.Đường tròn tâm I(4;-3),bán kính R=5.
D. Đường tròn tâm I(-4;3), bán kính R=5
Biết số phức z thỏa mãn điều kiện
3
≤
z
−
3
i
+
1
≤
5
. Tập hợp các điểm biểu diễn của z tạo thành một hình phẳng. Diện tích của hình phẳng đó bằng A.
16
π
B.
4
π
C.
9
π
D.
25
π
Đọc tiếp
Biết số phức z thỏa mãn điều kiện 3 ≤ z − 3 i + 1 ≤ 5 . Tập hợp các điểm biểu diễn của z tạo thành một hình phẳng. Diện tích của hình phẳng đó bằng
A. 16 π
B. 4 π
C. 9 π
D. 25 π