. Vậy 
Các câu hỏi tương tự
Biết \(\lim\limits_{x->+\infty}\) \(\left(\sqrt{25x^2+4\sqrt{2}+5}-5x\right)=\dfrac{a\sqrt{b}}{c}\) trong đó a,b,c là các số nguyên duơng, phân số \(\dfrac{a}{c}\) tối giản và \(a>1\). Tính \(S=a^2+b^2+c^2\)
Biết
lim
x
→
∞
(
x
+
1
)
2
x
+
1
5
x
3
+
x
+
2
-...
Đọc tiếp
Biết lim x → ∞ ( x + 1 ) 2 x + 1 5 x 3 + x + 2 = - a b trong đó a, b là các số nguyên dương và a b là phân số tối giản. Giá trị của tích ab bằng
A.30
B.42
C.10
D.36
Biết rằng
lim
x
→
-
∞
(
x
2
+
x
+
1
+
x
)
a
b
, (a là số nguyên, b là số nguyên dương,
a
b
tối giản). Tính giá trị biểu thức
P
...
Đọc tiếp
Biết rằng lim x → - ∞ ( x 2 + x + 1 + x ) = a b , (a là số nguyên, b là số nguyên dương, a b tối giản). Tính giá trị biểu thức P = a 2 + b 2
A. P = 5
B. P = 0
C. P = 1
D. P = -1
Biết
lim
x
→
-
∞
x
+
1
2
x
+
1
5
x
3
+
x
+
2...
Đọc tiếp
Biết lim x → - ∞ x + 1 2 x + 1 5 x 3 + x + 2 = - a b trong đó a, b là các số nguyên dương và a b là phân số tối giản. Giá trị của tích ab bằng.
A. 30
B. 42
C. 10
D. 36
Cho hàm số . Giá trị nhỏ nhất của hàm số trên là phân số tối giản
a
b
, ở đó a,b là số nguyên và b 0. Tính hiệu a-b. A. 50 B. -4 C. 4 D. -50
Đọc tiếp
Cho hàm số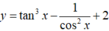 
. Giá trị nhỏ nhất của hàm số trên 
là phân số tối giản
a
b
, ở đó a,b là số nguyên và b > 0. Tính hiệu a-b.
A. 50
B. -4
C. 4
D. -50
Giá trị của k để hàm só f(x)=\(\hept{\begin{cases}\frac{x^{2019}+x-2}{\sqrt{2020+1}-\sqrt{x+2020}}\\2k\end{cases}}\) liên tục tại x0=1 có dạng \(k=\frac{a\sqrt{b}}{c}\), với a,b,c là các số nguyên và \(\frac{a\sqrt{b}}{c}\)
là phân số tới giản. tính a-b+c ( f(x) = 2k , khi x<=1; f(x)=... khi x>1)
1) gọi x là nghiệm trong khoảng left(pi;2piright) của phương trình cosxdfrac{sqrt{3}}{2} nếu biểu diễn xdfrac{api}{b} với a, b là 2 số nguyên và dfrac{a}{b} là phân số tối giản thì ab bằng bao nhiêu2) phương trình sinxdfrac{1}{2} có bao nhiêu nghiệm trên đoạn left[0;20piright]3) phương trình cos(x + 30độ ) dfrac{1}{2} có nghiệm là
Đọc tiếp
1) gọi x là nghiệm trong khoảng \(\left(\pi;2\pi\right)\) của phương trình \(cosx=\dfrac{\sqrt{3}}{2}\) nếu biểu diễn \(x=\dfrac{a\pi}{b}\) với a, b là 2 số nguyên và \(\dfrac{a}{b}\) là phân số tối giản thì ab bằng bao nhiêu
2) phương trình \(sinx=\dfrac{1}{2}\) có bao nhiêu nghiệm trên đoạn \(\left[0;20\pi\right]\)
3) phương trình \(cos\)(x + 30độ ) = \(\dfrac{1}{2}\) có nghiệm là
Biết
lim
x
→
8
x
+
1
-
2
x
-
7
x
-
1
-
7
-...
Đọc tiếp
Biết lim x → 8 x + 1 - 2 x - 7 x - 1 - 7 = - a b 7 trong đó a b là phân số tối giản, a và b là các số nguyên dương. Tổng a +b bằng
A. 8
B. 6
C. 4
D. 3
Số thập phân vô hạn tuần hoàn 0,32111... được biểu diễn dưới dạng phân số tối giản a/b, trong đó a,b là các số nguyên dương. Tính a - b.
A. 611
B. -611
C. 27901
D. -27901