Đáp án C
Ta thấy đồ thị của hàm số đi qua (0;0) nên ta loại đáp án A
Dựa vào chiều biến thiên của đồ thị hàm số => a > 0 ta loại đáp án B
Dựa vào số giao điểm của đồ thị hàm số với trục Ox ta chọn đáp án C
Đáp án C
Ta thấy đồ thị của hàm số đi qua (0;0) nên ta loại đáp án A
Dựa vào chiều biến thiên của đồ thị hàm số => a > 0 ta loại đáp án B
Dựa vào số giao điểm của đồ thị hàm số với trục Ox ta chọn đáp án C
Cho hàm số y = f x = x 3 − x + 1 và bốn hình vẽ lần lượt là 1, 2, 3, 4 dưới đây.
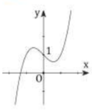
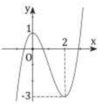
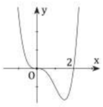
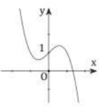
Đồ thị của hàm số y = f(x) là
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
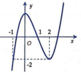
Cho hàm số y = f ( x ) = x 3 - 3 x 2 + 2 có đồ thị như hình vẽ bên. Trong bốn đường cong dưới đây, đường nào là đồ thị của hàm số y = x + 1 ?
A. 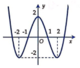
B. 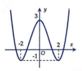
C. 
D. 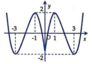
Cho hàm số y=f(x)=x^3+ax^2+bx+4 có đồ thị (C) như hình vẽ. Hỏi (C) là đồ thị của hàm số y=f(x) nào?
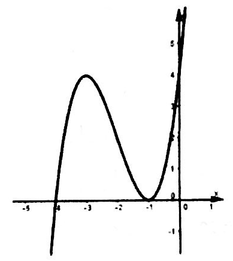
A. y = f ( x ) = x 3 - 3 x 2 + 4
B. y = f ( x ) = x 3 + 6 x 2 + 9 x + 4
C. y = f ( x ) = x 3 + 3 x 2 + 4
D. y = f ( x ) = x 3 - 6 x 2 + 9 x + 4
Hàm số y = x - 2 x 2 - 1 có đồ thị như hình vẽ bên.
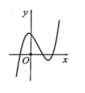
Hình nào dưới đây là đồ thị của hàm số y = x - 1 x 2 - x - 2
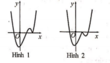
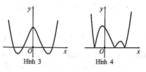
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
Hàm số y = ( x - 2 ) ( x 2 - 1 ) có đồ thị như hình vẽ bên.
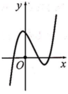
Hình nào dưới đây là đồ thị của hàm số y = x - 2 x 2 - 1
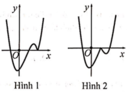
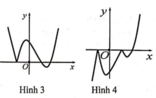
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
Hàm số y = ( x - 2 ) ( x 2 - 1 ) có đồ thị như hình vẽ bên.
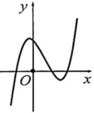
Hình nào dưới đây là đồ thị của hàm số y = x - 2 x 2 - 1

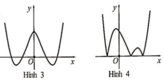
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
Hàm số y = x - 2 x 2 - 1 có đồ thị như hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số y = x + 1 x 2 - 3 x + 2 ?
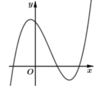
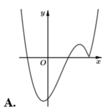
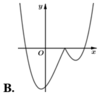
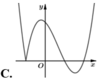
Hàm số y = x - 2 x 2 - 1 có đồ thị như hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số y = x + 1 x 2 - 3 x + 2 ?
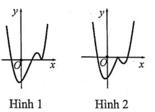
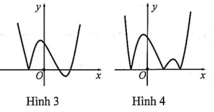
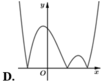
A. Hình 1.
B. Hình 2.
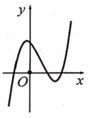
C. Hình 3.
D. Hình 4
Cho hàm số y = ( x - 1 ) ( x 2 - 4 ) có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số y = x - 1 ( x 2 - 4 ) là hình nào dưới đây?
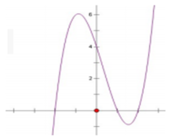
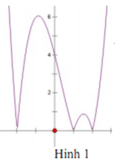
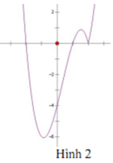
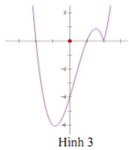
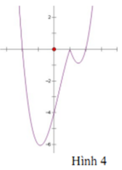
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
Cho hàm số f (x) có đồ thị của hàm số f'(x) như hình vẽ bên.
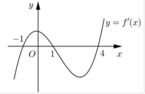
Biết f(-1)=f(4)=0. Hàm số y = ( f ( x ) ) 2 nghịch biến trên khoảng nào dưới đây ?
A. (-1;0).
B. (1;4).
C. ( - ∞ ; 1 ) .
D. ( 4 ; + ∞ ) .