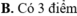Các câu hỏi tương tự
Cho hàm số
y
f
(
x
)
a
x
3
+
b
x
2
+
c
x
+
d
(
v
ớ
i
a
,
b
,
c
,
d
∈
ℝ
,
a...
Đọc tiếp
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d ( v ớ i a , b , c , d ∈ ℝ , a > 0 ) . Biết đồ thị hàm số y=f(x) này có điểm cực đại A (0;1) và điểm cực tiểu B(2;-3). Hỏi tập nghiệm của phương trình f 3 ( x ) + f ( x ) - 2 f ( x ) 3 = 0 có bao nhiêu phần tử?
A. 2019
B. 2018
C. 9
D. 8
Cho hàm số
y
f
(
x
)
ax
3
+
bx
2
+
cx
+
d
có hai cực trị
x
1
,
x
2
thỏa
-
2
x
1
0
x
2
2...
Đọc tiếp
Cho hàm số y = f ( x ) = ax 3 + bx 2 + cx + d có hai cực trị x 1 , x 2 thỏa - 2 < x 1 < 0 < x 2 < 2 và có đồ thị như hình vẽ.
Số điểm cực tiểu của hàm số ![]() là
là
A. 3.
B. 5.
C. 7.
D. 4.
Cho hàm số
y
f
(
x
)
a
x
3
+
b
x
2
+
c
x
+
d
có đồ thị (C). Biết đồ thị hàm số (C) có hai điểm cực trị A(2;-27) ; B(-4;81). Tính S-a+b-c+d
Đọc tiếp
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d có đồ thị (C). Biết đồ thị hàm số (C) có hai điểm cực trị A(2;-27) ; B(-4;81). Tính S=-a+b-c+d
![]()
![]()
![]()
![]()
Biết phương trình
a
x
3
+
b
x
2
+
c
x
+
d
0
a
≠
0
có đúng hai nghiệm thực. Hỏi đồ thị hàm số
y
a
x
3
+
b
x
2
+
c...
Đọc tiếp
Biết phương trình a x 3 + b x 2 + c x + d = 0 a ≠ 0 có đúng hai nghiệm thực. Hỏi đồ thị hàm số y = a x 3 + b x 2 + c x + d có bao nhiêu điểm cực trị?
A. 4
B. 5
C. 6
D. 3
Cho hàm số y ax3+ bx2+ cx+ d có đồ thị như hình vẽ bên. Đồ thị hàm số y |ax3+ bx2+ cx+ d + 1| có bao nhiêu điểm cực trị? A. 2 B. 3 C. 4 D. 5
Đọc tiếp
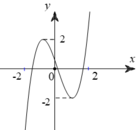
Cho hàm số y = ax3+ bx2+ cx+ d có đồ thị như hình vẽ bên. Đồ thị hàm số y = |ax3+ bx2+ cx+ d + 1| có bao nhiêu điểm cực trị?
A. 2
B. 3
C. 4
D. 5
Cho hàm số
f
x
a
x
3
+
b
x
2
+
c
x
+
d
có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số
y
f
-
2
x
2
+
4
x
A. 3 B. 4 C....
Đọc tiếp
Cho hàm số f x = a x 3 + b x 2 + c x + d
có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số y = f - 2 x 2 + 4 x
A. 3
B. 4
C. 2
D. 5
Cho hàm số y f(x) ax3+ bx2+cx+d có đạo hàm là hàm số y f’ (x) với đồ thị như hình vẽ bên. Biết rằng đồ thị hàm số y f( x) tiếp xúc với trục hoành tại điểm có hoành độ dương . Khi đó đồ thị hàm số y f( x) cắt trục tung tại điểm có tung độ là bao nhiêu? A. 2/3 B. 1 C. 3/2 D. 4/3
Đọc tiếp
Cho hàm số y= f(x) =ax3+ bx2+cx+d có đạo hàm là hàm số y= f’ (x) với đồ thị như hình vẽ bên. Biết rằng đồ thị hàm số y= f( x) tiếp xúc với trục hoành tại điểm có hoành độ dương . Khi đó đồ thị hàm số y= f( x) cắt trục tung tại điểm có tung độ là bao nhiêu?
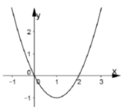
A. 2/3
B. 1
C. 3/2
D. 4/3
Biết
M
0
;
2
,
N
2
;
-
2
là các điểm cực trị của đồ thị hàm số
y
a
x
3
+
b
x
2
+
c
x
+
d
. Tính giá trị của hàm số tại
x...
Đọc tiếp
Biết M 0 ; 2 , N 2 ; - 2 là các điểm cực trị của đồ thị hàm số y = a x 3 + b x 2 + c x + d . Tính giá trị của hàm số tại x = 3
![]()
![]()
![]()
![]()
Cho hàm số
y
ax
3
+
bx
2
+
cx
+
d
với
a
≠
0
có hai hoành độ cực trị là x1 và x3. Tập hợp tất cả các giá trị của tham số m để phương trình f(x) f(m) có đúng ba nghiệm phân biệt là: A. . B. . C. . D. .
Đọc tiếp
Cho hàm số y = ax 3 + bx 2 + cx + d với a ≠ 0 có hai hoành độ cực trị là x=1 và x=3. Tập hợp tất cả các giá trị của tham số m để phương trình f(x) = f(m) có đúng ba nghiệm phân biệt là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.