Các câu hỏi tương tự
Biết đồ thị hàm số
y
2
m
-
n
x
2
+
m
x
+
1
x
2
+...
Đọc tiếp
Biết đồ thị hàm số y = 2 m - n x 2 + m x + 1 x 2 + m x + n - 6 (m, n là tham số) nhận trục hoành và trục tung làm hai đường tiệm cận. Tính m + n
A.-6
B.9
C.6
D.8
Biết đồ thị hàm số
y
2
x
−
n
x
2
+
m
x
+
1
x
2
+
m
x
+
n...
Đọc tiếp
Biết đồ thị hàm số y = 2 x − n x 2 + m x + 1 x 2 + m x + n − 6 (m, n là tham số) nhận trục hoành và trục tung làm hai đường tiệm cận. Tính m+n
A. 6
B. -6
C. 8
D. 9
Biết rằng đồ thị hàm số
y
(
n
-
3
)
x
+
n
-
2017
x
+
m
+
3
(m, n là tham số) nhận trục hoành làm tiệm cận ngang và nhận trục tung làm tiệm...
Đọc tiếp
Biết rằng đồ thị hàm số y = ( n - 3 ) x + n - 2017 x + m + 3 (m, n là tham số) nhận trục hoành làm tiệm cận ngang và nhận trục tung làm tiệm cận đứng. Tổng m+n bằng
A. 0
B. -3
C. 3
D. 6
Biết rằng đồ thị hàm số
y
n
-
3
x
+
n
-
2017
x
+
m
+
3...
Đọc tiếp
Biết rằng đồ thị hàm số y = n - 3 x + n - 2017 x + m + 3 (m,n là tham số) nhận trục hoành làm tiệm cận ngang và trục tung làm tiệm cận đứng. Tính tổng m-2n
A.0
B.-3
C.-9
D.6
Biết rằng đồ thị hàm
y
(
m
-
2
n
-
3
)
x
+
5
x
-
m
-...
Đọc tiếp
Biết rằng đồ thị hàm y = ( m - 2 n - 3 ) x + 5 x - m - n số nhận hai trục tọa độ làm hai đường tiệm cận. Tính tổng S = m 2 + n 2 - 2 .
A.S=2
B.S=0
C.S=-1
D.S=1
Biết rằng đồ thị hàm số
y
m
-
2
n
-
3
x
+
5
x
-
m
-
n
nhận hai trục tọa độ làm hai đường tiệm cận. Tính tổng
S...
Đọc tiếp
Biết rằng đồ thị hàm số y = m - 2 n - 3 x + 5 x - m - n nhận hai trục tọa độ làm hai đường tiệm cận. Tính tổng S = m 2 + n 2 - 2
A. S = -2
B. S = -1
C. S = 0
D. S = 2
Cho hàm số
y
x
-
3
x
-
m
2
+
1
(m là tham số;
m
≠
±
2
). Có bao nhiêu giá trị của tham số m để hình phẳng giới hạn bởi hai trục tọa độ và hai đường tiệm cận của đồ thị hàm số đã cho là một hình vuông. A. 1 B. 3 C. 2 D. 4...
Đọc tiếp
Cho hàm số y = x - 3 x - m 2 + 1 (m là tham số; m ≠ ± 2 ). Có bao nhiêu giá trị của tham số m để hình phẳng giới hạn bởi hai trục tọa độ và hai đường tiệm cận của đồ thị hàm số đã cho là một hình vuông.
A. 1
B. 3
C. 2
D. 4.
Biết rằng đồ thi của hàm số
y
(
a
-
3
)
x
+
a
+
2018
x
-
(
b
+
3
)
nhận trục hoành làm tiệm cận ngang và trục tung làm tiệm cân đứng. Khi đó...
Đọc tiếp
Biết rằng đồ thi của hàm số y = ( a - 3 ) x + a + 2018 x - ( b + 3 ) nhận trục hoành làm tiệm cận ngang và trục tung làm tiệm cân đứng. Khi đó giá trị của a+b là:
A. 3
B. -3
C. 6
D. 0
Cho hàm số y f(x) liên tục trên
ℝ
và có đồ thị như hình dưới. Biết rằng trục hoành là tiệm cận ngang của đồ thị. Tìm tất cả các giá trị thực của tham số m để phương trình
f
x
4
m
+
2
log
4
2
có hai nghiệm phân biệt dương. A. m 1 B. 0 m 1 C. m 0 D. 0 m 2
Đọc tiếp
Cho hàm số y = f(x) liên tục trên
ℝ
và có đồ thị như hình dưới. Biết rằng trục hoành là tiệm cận ngang của đồ thị. Tìm tất cả các giá trị thực của tham số m để phương trình
f
x
=
4
m
+
2
log
4
2
có hai nghiệm phân biệt dương.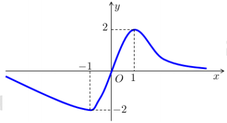
A. m > 1
B. 0 < m < 1
C. m < 0
D. 0 < m < 2



