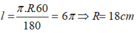Các câu hỏi tương tự
Hình bên là hình nón .chiều cao là h(cm),bán kính đường tròn đáy là r(cm) và độ dài đường sinh là m(cm) thì thể tích hình nón này là:A.
π
.
r
2
h (
c
m
3
) B. (1/3)
π
.
r
2
h (
c
m...
Đọc tiếp
Hình bên là hình nón .chiều cao là h(cm),bán kính đường tròn đáy là r(cm) và độ dài đường sinh là m(cm) thì thể tích hình nón này là:
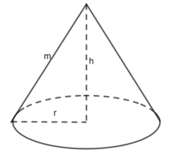
A. π . r 2 h ( c m 3 ) B. (1/3) π . r 2 h ( c m 3 )
C. π .r.m ( c m 3 ) D. π r(r+m) ( c m 3 )
Cho đường tròn tâm O, bán kính R = 13 cm. Dây AB của đường tròn cách O một khoảng bằng 5 cm có độ dài là
A. 24cm B. 18cm C. 16cm D.12cm
Giải chi tiết được ko ạ?
cho đường tròn (o) bán kính R đường kính AB dây cung AC, tiếp tuyến với đường tròn tại B và C cắt nhau ở D
a) CM: DO//AC
b) biết góc BAC = 30 độ bán kính 2 cm tính BD và CD
Tính độ dài AB của đường tròn O bán kính R theo r biết số đo cung nhỏ AB = a) 150 độ ,b) 45 độ ,c) 135 độ
Lấy giá trị gần đúng của π là 3,14, hãy điền vào các ô trống trong bảng (đơn vị độ dài: cm, làm tròn kết quả đến chữ số thập phân thứ hai):
Bán kính R của đường tròn
10
3
Đường kính d của đường tròn
10
3
Độ dài C của đường tròn
20
25,12
Đọc tiếp
Lấy giá trị gần đúng của π là 3,14, hãy điền vào các ô trống trong bảng (đơn vị độ dài: cm, làm tròn kết quả đến chữ số thập phân thứ hai):
| Bán kính R của đường tròn | 10 | 3 | ||||
| Đường kính d của đường tròn | 10 | 3 | ||||
| Độ dài C của đường tròn | 20 | 25,12 |
Lấy giá trị gần đúng của π là 3,14, hãy điền vào các ô trống trong bảng (đơn vị độ dài: cm, làm tròn kết quả đến chữ số thập phân thứ hai):
Bán kính R của đường tròn
10
3
Đường kính d của đường tròn
10
3
Độ dài C của đường tròn
20
25,12
Đọc tiếp
Lấy giá trị gần đúng của π là 3,14, hãy điền vào các ô trống trong bảng (đơn vị độ dài: cm, làm tròn kết quả đến chữ số thập phân thứ hai):
| Bán kính R của đường tròn | 10 | 3 | ||||
| Đường kính d của đường tròn | 10 | 3 | ||||
| Độ dài C của đường tròn | 20 | 25,12 |
Cho hai đường tròn (O; R) và (O'; r) ở ngoài nhau. Gọi MN là tiếp tuyến chung ngoài, EF là tiếp tuyến chung trong (M và E thuộc (O), N và F thuộc (O')). Tính bán kính của đường tròn (O) và (O') trong các trường họp sau:
a, OO' = 10 cm, MN = 8cm và EF = 6 cm
b, OO' = 13 cm, MN = 12 cm và EF = 5 cm
trên hình tròn (O;R)biết độ dài một cung tròn 30 độ là π(cm ) thì diện tích một hình quạt tròn cung 60 độ là ???
cho đường tròn tâm O, bán kính R, dây cung AB=R. TRên tia đối của tia BA lấy C sao cho BC=BA. Tia CO cắt đường tròn tâm O tại D. R=3 cm
a, tính góc ACD
b, tính CD
Cho đường tròn (O; R) đường kính AB. Trên các bán kính OA, OB lần lượt lấy các điểm M và N sao cho OM = ON. Qua M, N vẽ các dây cung CD, EF song song với nhau( C, E thuộc nửa đường tròn đường kính AB).
a) CMR: tứ giác CDFE là hình chữ nhật
b) Cho CM = 2/3 R, góc giữa CD và OA= 60 độ. Tính diện tích tứ giác CDFE