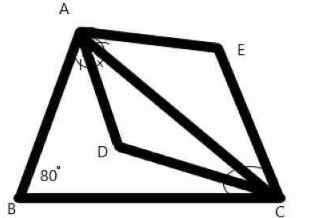
a) \(\Delta ACD\) có \(\widehat{D}+\widehat{A_2}+\widehat{C_2}=180^o\)
\(\Delta ACE\) có \(\widehat{E}+\widehat{A_3}+\widehat{C_3}=180^o\)
Mà \(\widehat{A_2}=\widehat{A_3},\widehat{C_2}=\widehat{C_3}\) nên \(\widehat{D}=\widehat{E}\)
b) \(\Delta ABC\) có \(\widehat{B}+\widehat{BAC}+\widehat{BCA}=180^o\Rightarrow\widehat{BAC}+\widehat{BCA}=180^o-\widehat{B}=180^o-80^o=100^o\)
\(\widehat{BAE}+\widehat{BCE}=\dfrac{3}{2}\widehat{BAC}+\dfrac{3}{2}\widehat{BCA}=\dfrac{3}{2}\left(\widehat{BAC}+\widehat{BCA}\right)=\dfrac{3}{2}.100^o=150^o\)
Tứ giác ABCE có \(\widehat{B}+\widehat{BAE}+\widehat{E}+\widehat{BCE}=360^o\Rightarrow\widehat{B}+\widehat{E}=360^o-\left(\widehat{BAE}+\widehat{BCE}\right)=360^o-150^o=210^o\)