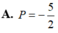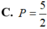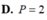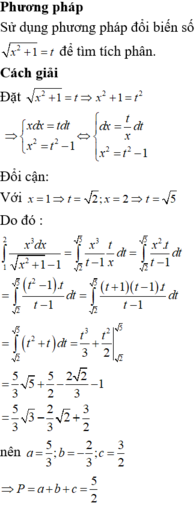Các câu hỏi tương tự
Biết
∫
3
4
d
x
(
x
+
1
)
(
x
-
2
)
a
ln
2
+
b
ln
5
+
c
, với a,b,c là...
Đọc tiếp
Biết ∫ 3 4 d x ( x + 1 ) ( x - 2 ) = a ln 2 + b ln 5 + c , với a,b,c là các số hữu tỉ. Tính S = a - 3b + c
A. S = 3
B. S = 2
C. S = -2
D. S = 4
Biết
∫
π
4
π
3
cos
2
x
+
sin
x
cos
x
+
1
cos
4
x
+
sin
x...
Đọc tiếp
Biết ∫ π 4 π 3 cos 2 x + sin x cos x + 1 cos 4 x + sin x cos 3 x d x = a + b ln 2 + c ln ( 1 + 3 ) ,
với a, b, c là các số hữu tỉ. Giá trị của abc bằng:
A. 0
B. -2
C. -4
D. -6
Biết
∫
1
3
d
x
1
+
x
+
1
+
x
2
a
3
+
b
2
+
c
+
1
2...
Đọc tiếp
Biết ∫ 1 3 d x 1 + x + 1 + x 2 = a 3 + b 2 + c + 1 2 ln ( 3 2 - 3 ) với a, b, c là các số hữu tỷ.
Tính P = a + b + c.
![]()
![]()
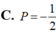
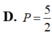
Cho hàm số f(x) xác định trên
(
-
∞
;
-
1
)
∪
(
0
;
+
∞
)
và
f
(
x
)
1
x
2
+
x
;
f
(
1
)
ln...
Đọc tiếp
Cho hàm số f(x) xác định trên ( - ∞ ; - 1 ) ∪ ( 0 ; + ∞ ) và f ' ( x ) = 1 x 2 + x ; f ( 1 ) = ln 1 2 Biết ∫ 1 2 x 2 + 1 f ( x ) d x = a ln 3 + b ln 2 + c với a,b,c là các số hữu tỉ. Giá trị biểu thức a+b+c bằng
A. 27/2
B. 1/6
C. 7/6
D. -3/2
Cho hàm số
y
f
(
x
)
liên tục trên
R
{
-
1
;
0
}
thỏa mãn
f
(
1
)
2
ln
2
+
1
,
x
(
x
+
1
)
f
(
x
)
+
(
x
+
2
)
f...
Đọc tiếp
Cho hàm số y = f ( x ) liên tục trên R \ { - 1 ; 0 } thỏa mãn f ( 1 ) = 2 ln 2 + 1 , x ( x + 1 ) f ' ( x ) + ( x + 2 ) f ( x ) = x ( x + 1 ) , ∀ x ∈ R \ { - 1 ; 0 } Biết f ( 2 ) = a + b ln 3 với a, b là hai số hữu tỉ. Tính T = a 2 - b
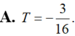
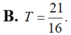
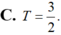
![]()
Tích phân
∫
1
2
x
ln
x
d
x
(
x
2
+
1
)
2
a
ln
2
+
b
ln
3
+
c
ln
5
(với a,b,c là các số hữu tỉ). Tính tổng a+b+c
Đọc tiếp
Tích phân ∫ 1 2 x ln x d x ( x 2 + 1 ) 2 = a ln 2 + b ln 3 + c ln 5 (với a,b,c là các số hữu tỉ). Tính tổng a+b+c
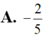
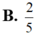
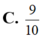
Biết
∫
1
2
x
ln
(
x
2
+
1
)
d
x
a
ln
5
+
b
ln
2
+
c
với a, b, c là các số hữu tỉ. Tính P a + b + c.
Đọc tiếp
Biết ∫ 1 2 x ln ( x 2 + 1 ) d x = a ln 5 + b ln 2 + c với a, b, c là các số hữu tỉ. Tính P = a + b + c.
![]()
![]()
![]()
![]()
Biết
∫
π
4
π
3
1
cos
4
x
+
sin
x
co
s
3
x
d
x...
Đọc tiếp
Biết ∫ π 4 π 3 1 cos 4 x + sin x co s 3 x d x = a - b + c ln 2 + d ln ( 1 + 3 ) với a,b,c,d là các số hữu tỉ. Giá trị của abcd bằng
A. 0
B. -36
C. -24
D. -6
hàm số
f
(
x
)
ln
1
-
1
x
2
. Biết rằng
f
(
2
)
+
F
(
3
)
+
.
.
.
+
f
(
2018
)
ln
a
-
ln
b...
Đọc tiếp
hàm số f ( x ) = ln 1 - 1 x 2 . Biết rằng f ( 2 ) + F ( 3 ) + . . . + f ( 2018 ) = ln a - ln b + ln c - ln d với a, b, c, d là các số nguyên dương, trong đó a, c, d là các số nguyên tố và a<b<c<d. Tính P=a+b+c+d
A. 1986
B. 1698
C. 1689
D. 1968