Đáp án A
Phương pháp:
Đặt ẩn phụ.
Cách giải:
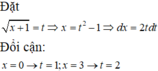
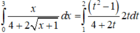
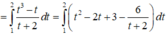
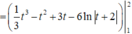
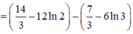
![]()
![]()
Đáp án A
Phương pháp:
Đặt ẩn phụ.
Cách giải:
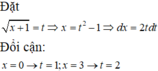
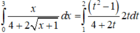
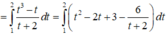
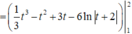
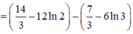
![]()
![]()
Tính các nguyên hàm.
a)\(\int\dfrac{2dx}{x^2-5x}=A\ln\left|x\right|+B\ln\left|x-5\right|+C\) . Tìm 2A-3B.
b)\(\int\dfrac{x^3-1}{x+1}\)dx=\(Ax^3-Bx^2+x+E\ln\left|x+1\right|+C\).Tính A-B+E
Giải các bất phương trình sau:
a) (2x − 7)ln(x + 1) > 0;
b) (x − 5)(logx + 1) < 0;
c) 2 log 3 2 x + 5 log 2 2 x + log 2 x – 2 ≥ 0
d) ln(3 e x − 2) ≤ 2x
Cho hàm số f ( x ) = ln ( 1 - 4 ( 2 x - 1 ) 2 ) . Biết rằng f ( 2 ) + f ( 3 ) + . . . + f ( 2020 ) = ln a b , trong đó a b là phân số tối giản, a , b ∈ N * . Tính b -3a
A. -2
B. 3
C. -1
D. 1
Cho hàm số f ( x ) = ln 1 - 4 ( 2 x - 1 ) 2 . Biết rằng ,f(2) + f(3) + ....+f(2020) = ln a b trong đó a b , là phân số tối giản, a, b ∈ ℕ * . Tính b - 3a
A. -2
B. 3
C. -1
D. 1
hàm số f ( x ) = ln 1 - 1 x 2 . Biết rằng f ( 2 ) + F ( 3 ) + . . . + f ( 2018 ) = ln a - ln b + ln c - ln d với a, b, c, d là các số nguyên dương, trong đó a, c, d là các số nguyên tố và a<b<c<d. Tính P=a+b+c+d
A. 1986
B. 1698
C. 1689
D. 1968
Trong các hàm số dưới đây, hàm số nào là một nguyên hàm của hàm số f x = 1 1 + sinx
a) F(x) = 1 - cos x 2 + π 4
b) G(x) = 2 tan x 2
c) H(x) = ln(1 + sinx)
d) K(x) = 2 1 - 1 1 + tan x 2
Trong không gian OxyzOxyz cho hai điểm A(2;4;3)A(2;4;3) và B(2;7;1)B(2;7;1). Trong các phương trình dưới đây, phương trình nào là phương trình tham số của đường thẳng ABAB? (với t\in \Rt∈R)
A,\left\{{}\begin{matrix}x=2+2t\\y=7+4t\\z=1+3t\end{matrix}\right.⎩⎪⎨⎪⎧x=2+2ty=7+4tz=1+3t
B,\left\{{}\begin{matrix}x=4\\y=3+3t\\z=2-2t\end{matrix}\right.⎩⎪⎨⎪⎧x=4y=3+3tz=2−2t
c,\left\{{}\begin{matrix}x=2\\y=4-3t\\z=3+2t\end{matrix}\right.⎩⎪⎨⎪⎧x=2y=4−3tz=3+2t
d,\left\{{}\begin{matrix}x=2+2t\\y=4+7t\\z=3+t\end{matrix}\right.⎩⎪⎨⎪⎧x=2+2ty=4+7tz=3+t
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(-4;2;-1) và đường thẳng d: x = - 1 + t y = 3 - t z = t . Gọi A'(a;b;c) là điểm đối xứng với A qua d. Tính a + b + c.
A. -2
B. -1
C. 1
D. 5
Trong không gian Oxyz, cho hai điểm A(1;-1;2),B(3;-4;-2)và đường thẳng
d : x = 2 + 4 t y = - 6 t z = - 1 - 8 t . Điểm I(a,b,c) thuộc d là điểm thỏa mãn IA + IB đạt giá trị nhỏ nhất. Khi đó T = a + b + c bằng
A. 23 58
B. - 43 58
C. 65 29
D. - 21 58