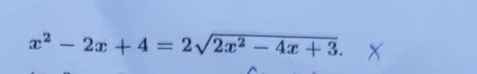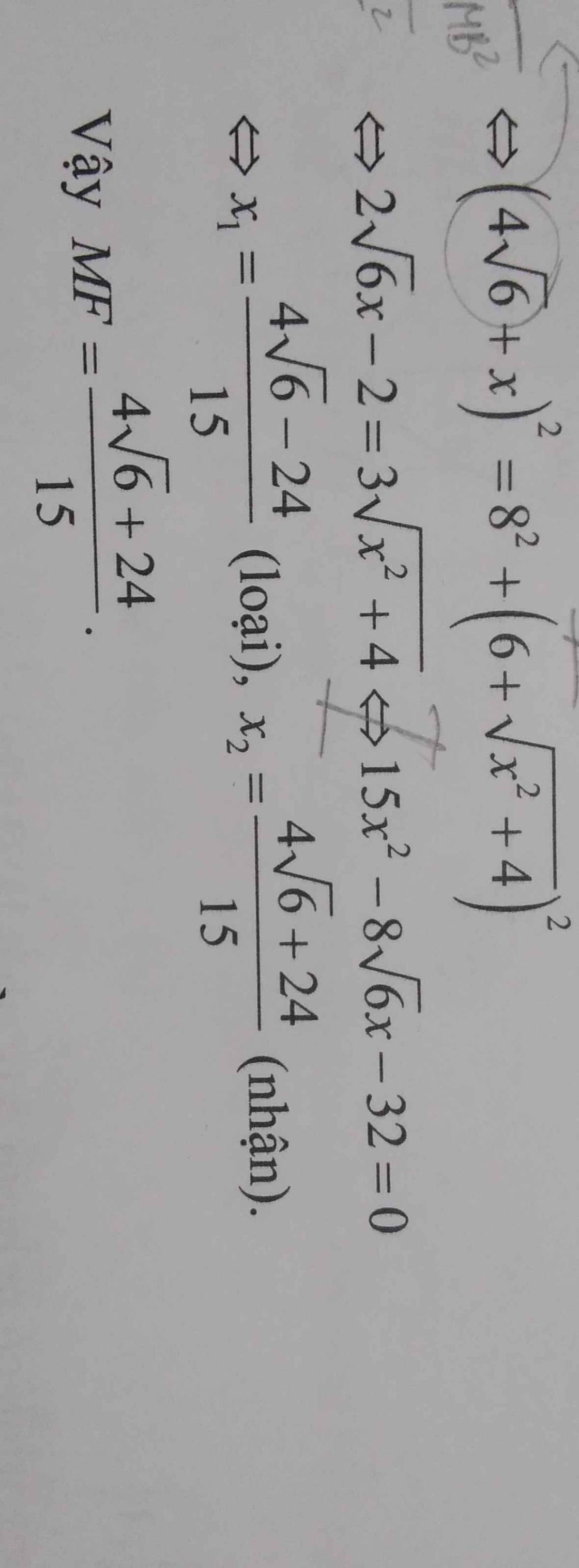Question

  Bài này khi sáng thi HSG em giải ra vô nghiệm, mn giải giúp em với ạ

Answer 1

Ta có: \(x^2-2x+4=2\sqrt{2x^2-4x+3}\)

=>\(x^2-2x+4=2\sqrt{2x^2-4x+8-5}\)

=>\(x^2-2x+4=2\sqrt{2\left(x^2-2x+4\right)-5}\)

Đặt \(x^2-2x+4=a\left(a>=3\right)\)

Phương trình ban đầu sẽ trở thành

\(2\sqrt{2a-5}=a\)

=>\(\sqrt{8a-20}=a\)

=>\(\left\{{}\begin{matrix}8a-20=a^2\\a>=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a^2-8a+20=0\\a>=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}a^2-8a+16+4=0\\a>=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(a-4\right)^2+4=0\left(vôlý\right)\\a>=0\end{matrix}\right.\)

=>\(a\in\varnothing\)

=>\(x\in\varnothing\)