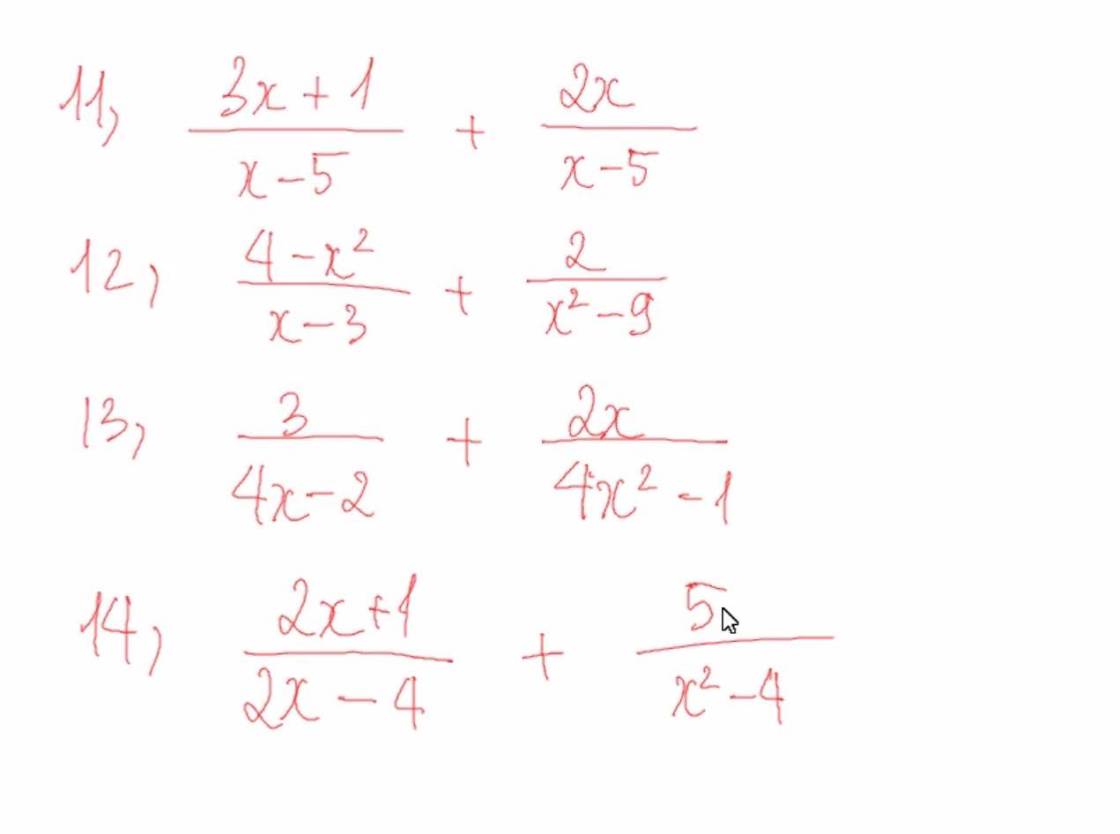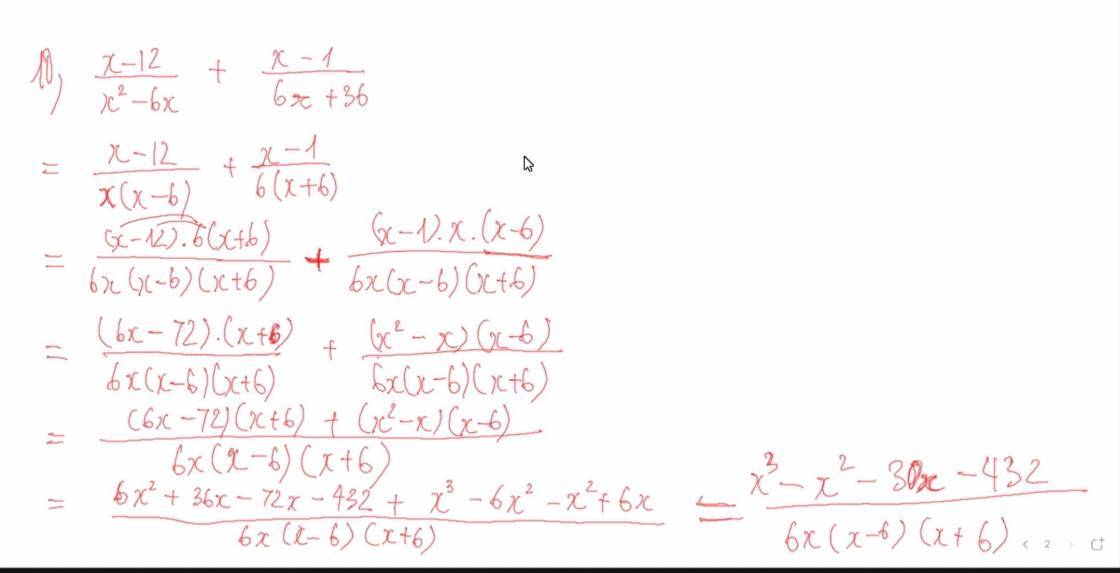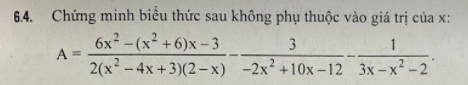do tam giác ABC có góc A=90\(^o\)=>\(\Delta ABC\) vuông tại A
\(\Delta ABH\sim\Delta CBA\left(g.g\right)\)( vì góc B chung, góc AHB=góc BAC)
\(=>\dfrac{AB}{BC}=\dfrac{BH}{BA}=>AB^2=BH.BC\)(1)
b,dựa vào (1)\(=>AB=\sqrt{BH.BC}=\sqrt{BH\left(BH+HC\right)}=\sqrt{4.\left(4+9\right)}=2\sqrt{13}cm\)
theo pytago\(=>AC=\sqrt{BC^2-AB^2}=\sqrt{13^2-\left(2\sqrt{13}\right)^2}=3\sqrt{13}cm\)
c,theo tính chất phan giác=>\(\dfrac{AB}{BC}=\dfrac{AD}{DC}=>\dfrac{AD}{DC}=\dfrac{2}{3}\)\(=>DC=\dfrac{3}{2}AD\)
có: \(AD+DC=AC=>AD+\dfrac{3}{2}AD=3\sqrt{13}=>AD=\dfrac{6\sqrt{13}}{5}cm\)
\(=>S\left(\Delta DBA\right)=\dfrac{AB.AD}{2}=15,6cm^2\)
có: tam giac BDA đồng dạng tam giác BEH(g.g)(do góc B1=góc B2, góc A=góc H=90 độ)
=>góc E2= góc D1
mà góc E2=góc E1(đối đỉnh)=>góc D1=góc E1=>tam giác AED cân tại A
=>AE=AD=\(\dfrac{6\sqrt{13}}{5}cm\),
theo pytago=>AH=\(\sqrt{AB^2-BH^2}=\sqrt{ \left(2\sqrt{13}\right)^2-4^2}=6cm\)
=>EH=AH-AE=\(6-\dfrac{6\sqrt{13}}{5}cm\)
=>\(S\left(\Delta EBH\right)=\dfrac{1}{2}BH.EH\) rồi tự tính ra rồi lập tỉ số 2 S tam giác (mỏi tay)