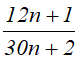Để \(\dfrac{12.n+1}{30.n+2}\) là p/s tối giản thì 12.n+1 và 30.n+2 phải nguyên tố với nhau
Ta có:Gọi d=ƯCLN(12.n+1;30.n+2)
\(=>\left\{{}\begin{matrix}\left(12.n+1\right)⋮d\\\left(30.n+2\right)⋮d\end{matrix}\right.=>\left\{{}\begin{matrix}\left[5.\left(12.n+1\right)\right]⋮d\\\left[2.\left(30.n+2\right)\right]⋮d\end{matrix}\right.\)
\(=>\left\{{}\begin{matrix}\left(60.n+5\right)⋮d\\\left(60.n+4\right)⋮d\end{matrix}\right.\)
=>[(60.n+5)-(60.n+4)]⋮d=>1⋮d
Thay d vào ƯCLN(12.n+1;30.n+2)
=>ƯCLN(12.n+1;30.n+2)=1
=>12.n+1 và 30.n+2 nguyên tố với nhau
=>\(\dfrac{12.n+1}{30.n+2}\) là p/s tối giản với mọi số nguyên n