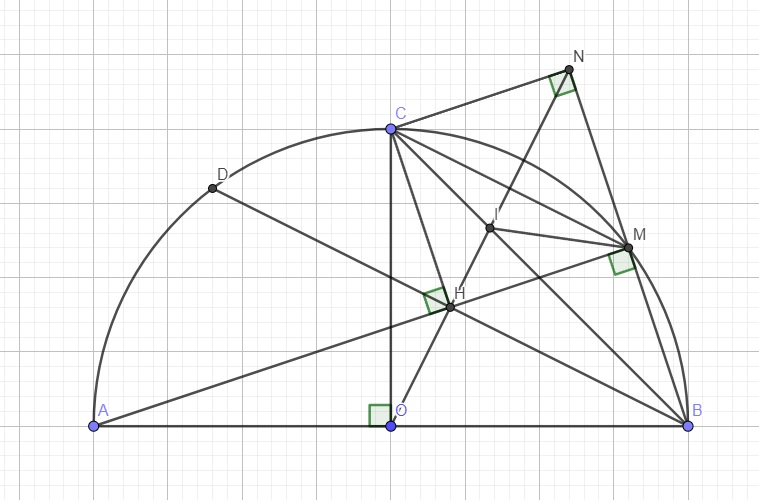
Bài 29. Cho nửa đường tròn (O;R) đường kính AB.Từ O kẻ đường thẳng vuông góc với AB và cắt nửa đường tròn (O) tại điểm C .Trên cung CB lấy một điểm M bất kì .Kẻ CH vuông góc với AM tại H .Gọi N là giao điểm của OH và MB a) Chứng minh tứ giác CHOA nội tiếp đường tròn b) Chứng minh CAO=ONB=45° c) OH cắt CB tại điểm I và MI cắt nửa (O) tại điểm thứ 2 là D. Chứng minh CM//BD d) Xác định vị trí của M để ba điểm D,H,B thẳng hàng Giúp mình với ạ,mình cần gấp!
a.
Theo giả thiết \(\left\{{}\begin{matrix}CO\perp AB\\CH\perp AM\end{matrix}\right.\) \(\Rightarrow\widehat{AHC}=\widehat{AOC}=90^0\)
\(\Rightarrow\) O và H cùng nhìn AC dưới 1 góc vuông nên CHOA nội tiếp
b.
\(\left\{{}\begin{matrix}\widehat{AOC}=90^0\\OA=OC=R\end{matrix}\right.\) \(\Rightarrow\Delta OAC\) vuông cân tại O
\(\Rightarrow\widehat{CAO}=\widehat{ACO}=45^0\)
Theo câu a, CHOA nội tiếp \(\Rightarrow\widehat{AHO}=\widehat{ACO}=45^0\) (cùng chắn AO)
\(\Rightarrow\widehat{NHM}=\widehat{AHO}=45^0\) (đối đỉnh)
\(\widehat{AMB}=90^0\) (góc nt chắn nửa đường tròn) \(\Rightarrow\widehat{ONB}=90^0-\widehat{NHM}=45^0\)
c.
\(OB=OC=R\Rightarrow\Delta OBC\) vuông cân tại O \(\Rightarrow\widehat{OCB}=45^0\)
\(\Rightarrow\widehat{OCB}=\widehat{ONB}\Rightarrow OCNB\) nội tiếp
\(\Rightarrow\widehat{CNB}+\widehat{COB}=180^0\Rightarrow\widehat{CNB}=90^0\)
\(\Rightarrow CNMH\) là hình chữ nhật (tứ giác có 3 góc vuông)
Theo cm câu b, \(\widehat{NHM}=\widehat{ONB}=45^0\Rightarrow\Delta HNM\) cân tại M
\(\Rightarrow HM=NM\Rightarrow CNMH\) là hình vuông
\(\Rightarrow HN\) là trung trực của CM
\(\Rightarrow IC=IM\) \(\Rightarrow\Delta ICM\) cân tại I
\(\Rightarrow\widehat{ICM}=\widehat{IMC}\)
Mà \(\widehat{IMC}=\widehat{CBD}\) (cùng chắn CD)
\(\Rightarrow\widehat{ICM}=\widehat{CBD}\)
\(\Rightarrow\) CM song song BD (hai góc so le trong bằng nhau)
d.
Giả sử D, H, B thẳng hàng
Theo câu c, CM song song BD \(\Rightarrow CM||BH\)
\(\Rightarrow\widehat{BHM}=\widehat{HMC}=45^0\) (so le trong)
\(\Rightarrow\Delta BMH\) vuông cân tại M
\(\Rightarrow BM=MH\)
\(\Rightarrow BM=HM=NM=CN\) (do CNMH là hình vuông theo cmt)
\(\Rightarrow BN=2BM\)
Áp dụng định lý Pitago cho tam giác OBC:
\(BC^2=OB^2+OC^2=2R^2\)
Áp dụng Pitago cho tam giác BCN:
\(BC^2=CN^2+BN^2\)
\(\Rightarrow2R^2=BM^2+\left(2BM\right)^2\)
\(\Rightarrow2R^2=5BM^2\)
\(\Rightarrow BM^2=\dfrac{2R^2}{5}\)
\(\Rightarrow BM=\dfrac{R\sqrt{10}}{5}\)
Vậy để D, H, B thẳng hàng thì M nằm ở vị trí trên cung BC sao cho \(BM=\dfrac{R\sqrt{10}}{5}\)