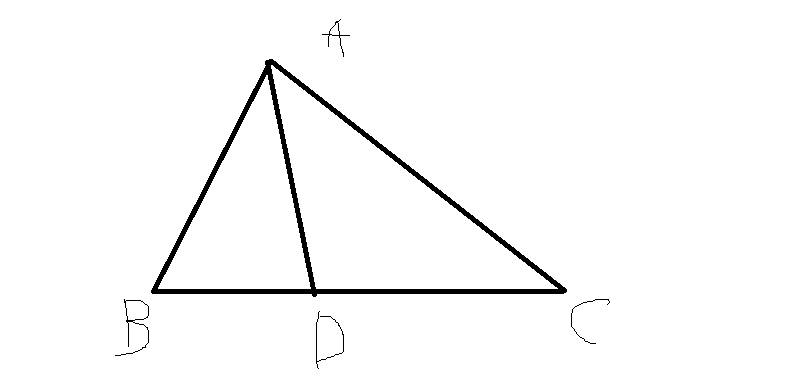
xét tam giác ABC có AD là phân giác góc A (gt)
\(=>\dfrac{AB}{AC}=\dfrac{DB}{DC}\) (tính chất đường phân giác)
\(=>\dfrac{DB}{DC}=\dfrac{9}{12}\\ =>\dfrac{DB}{DC}=\dfrac{3}{4}\)
\(=>\dfrac{DB}{9}=\dfrac{DC}{4}\)
mà BC=DB+DC=15 nên áp dụng tính chất dãy tỉ số bằng nhau ta có
\(\dfrac{DB}{9}=\dfrac{DC}{4}=\dfrac{DB+DC}{9+4}=\dfrac{BC}{13}=\dfrac{15}{13}\\ =>DB=\dfrac{15}{13}\cdot9=\dfrac{135}{13}\\ DC=\dfrac{15}{13}\cdot4=\dfrac{60}{13}\)