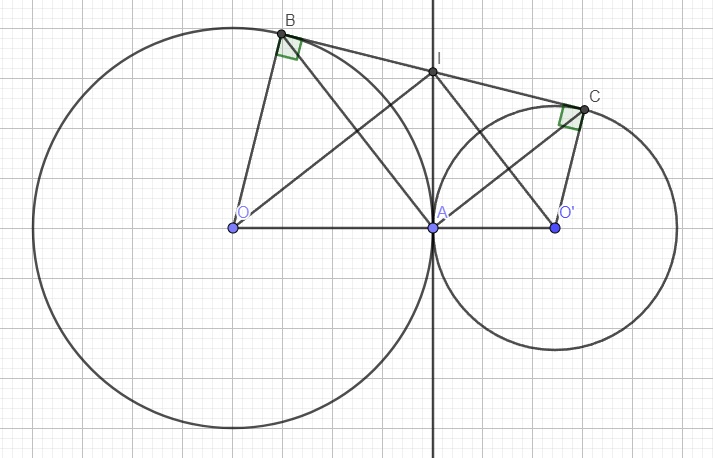
a.
Do IA và IB là tiếp tuyến của (O), theo t/c hai tiếp tuyến cắt nhau ta có: \(IA=IB\)
Tương tự, IA và IC là tiếp tuyến của (O') \(\Rightarrow IA=IC\)
\(\Rightarrow IA=IB=IC=\dfrac{1}{2}BC\)
\(\Rightarrow\Delta ABC\) vuông tại A
\(\Rightarrow\widehat{BAC}=90^0\)
b.
Theo t/c hai tiếp tuyến cắt nhau ta có:
\(\left\{{}\begin{matrix}\widehat{OIB}=\widehat{OIA}=\dfrac{1}{2}\widehat{BIA}\\\widehat{O'IC}=\widehat{O'IA}=\dfrac{1}{2}\widehat{CIA}\end{matrix}\right.\)
\(\Rightarrow\widehat{OIA}+\widehat{O'IA}=\dfrac{1}{2}\left(\widehat{BIA}+\widehat{CIA}\right)\)
\(\Rightarrow\widehat{OIO'}=\dfrac{1}{2}.\widehat{BIC}=\dfrac{1}{2}.180^0=90^0\)
\(\Rightarrow\Delta OIO'\) vuông tại O
Do IA là tiếp tuyến chung tại điểm tiếp xúc ngoài của 2 đường tròn \(\Rightarrow IA\perp O'O\)
Áp dụng hệ thức lượng trong tam giác vuông OIO' với đường cao IA:
\(IA^2=OA.O'A=36\Rightarrow IA=6\left(cm\right)\)
\(\Rightarrow BC=2IA=12\left(cm\right)\)