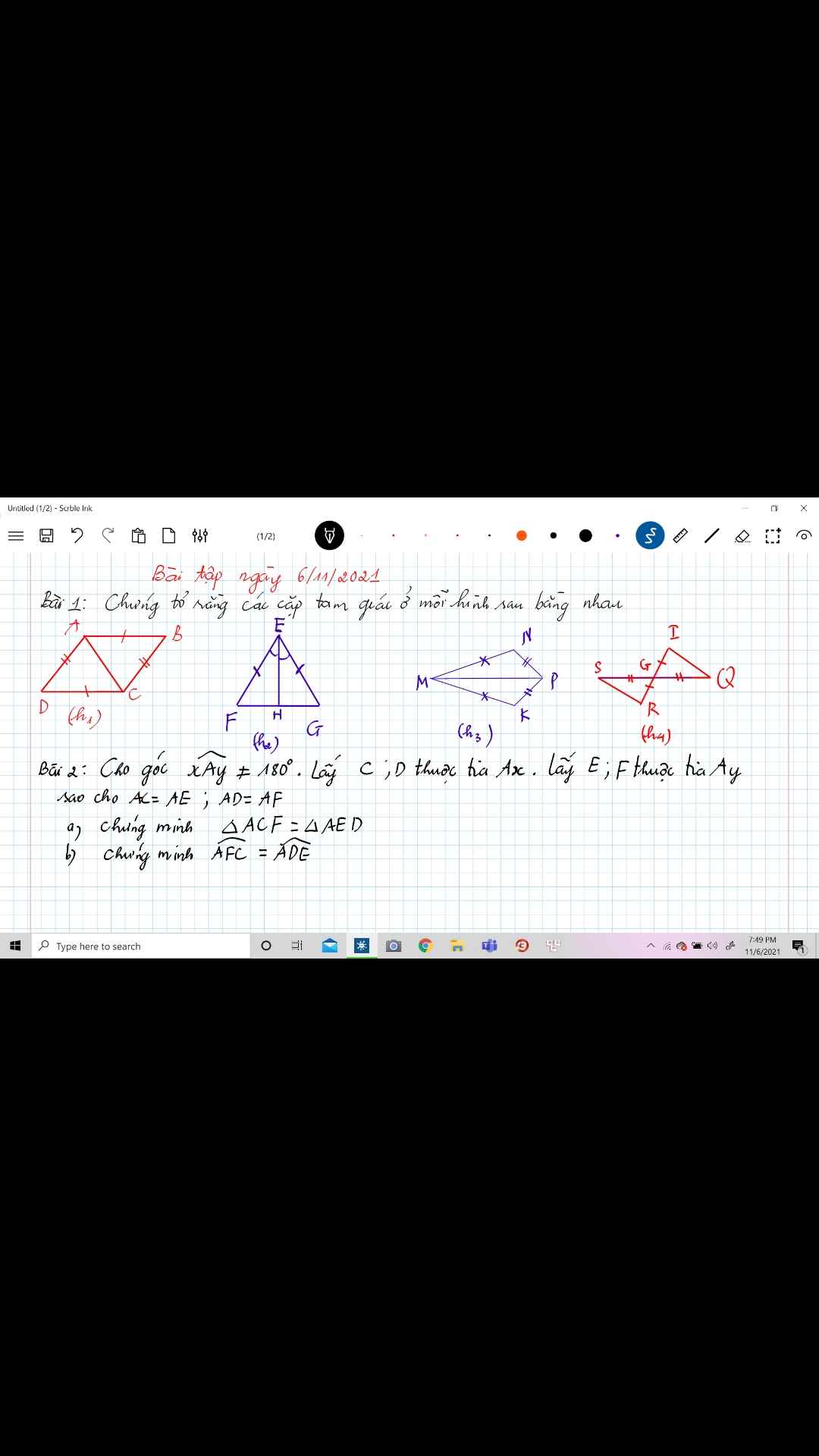
1:
\(A=\dfrac{2}{3}+\dfrac{8}{9}+...+\dfrac{3^n-1}{3^n}\)
\(=1-\dfrac{1}{3}+1-\dfrac{1}{3^2}+...+1-\dfrac{1}{3^n}\)
\(=n-\left(\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^n}\right)\)
Đặt \(B=\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^n}\)
=>\(3B=1+\dfrac{1}{3^1}+...+\dfrac{1}{3^{n-1}}\)
=>\(2B=1+\dfrac{1}{3}+...+\dfrac{1}{3^{n-1}}-\dfrac{1}{3}-\dfrac{1}{3^2}-...-\dfrac{1}{3^n}=1-\dfrac{1}{3^n}\)
=>\(2B=\dfrac{3^n-1}{3^n}\)
=>\(B=\dfrac{1}{2}-\dfrac{1}{2\cdot3^n}< \dfrac{1}{2}\)
\(A=n-\left(\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^n}\right)\)
\(=n-B>n-\dfrac{1}{2}\)












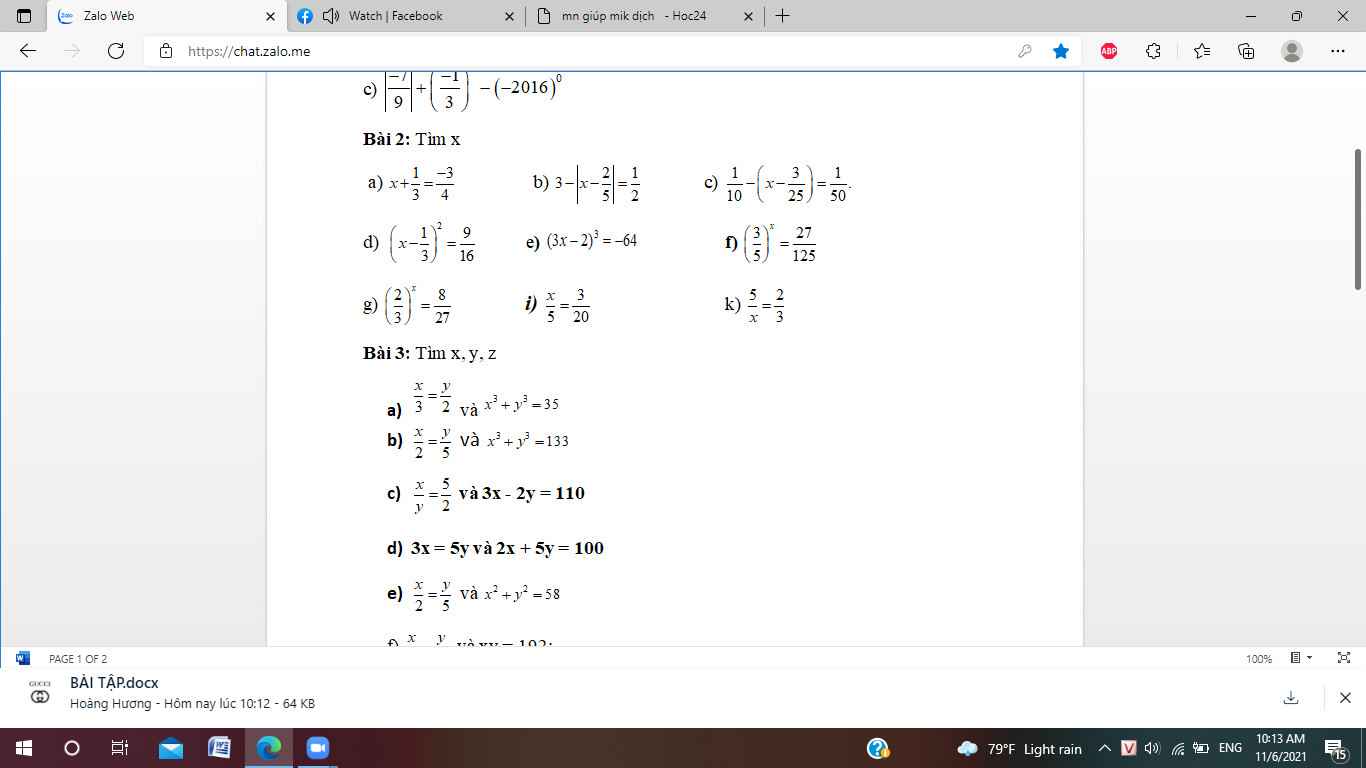
 mn giúp mik vs mik cần gấp( có trình bày nha~)
mn giúp mik vs mik cần gấp( có trình bày nha~)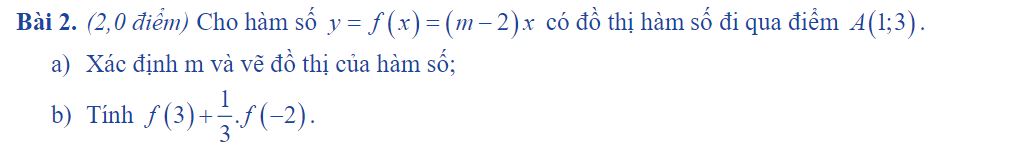 mn giúp mik vs mik cần gấp( có trình bày đồ thị nha)
mn giúp mik vs mik cần gấp( có trình bày đồ thị nha)