Các câu hỏi tương tự
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Góc giữa hai đường thẳng AB′ và BC′ bằng (tham khảo hình vẽ bên).
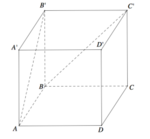
A. 60 °
B. 90 °
C. 45 °
D. 300 °
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Góc giữa hai đường thẳng AB′ và BC′ bằng (tham khảo hình vẽ bên). A.
60
°
B.
90
°
C.
45
°
D.
30
°
Đọc tiếp
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Góc giữa hai đường thẳng AB′ và BC′ bằng (tham khảo hình vẽ bên).

A. 60 °
B. 90 °
C. 45 °
D. 30 °
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng 1. Gọi K là trung điểm của DD′ (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng CK và A′D bằng A.
10
5
B.
4
5
C.
10
10
D.
2
5
Đọc tiếp
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng 1. Gọi K là trung điểm của DD′ (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng CK và A′D bằng
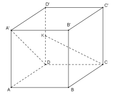
A. 10 5
B. 4 5
C. 10 10
D. 2 5
Cho nửa đường tròn tâm O, đường kính AB ,vẽ điểm S ở bên ngoài nửa đường tròn sao cho hai đoạn thẳng AS và BS cắt nửa đường tròn nói trên tại C và D .AD cắt BC tại H , hai đường thẳng AB và SH cắt nhau tại E.a) chứng minh tứ giác ACHE nội tiếp đường trònb) chứng minh hai góc HED va HBD bằng nhau c) chứng minh hai góc CEH va HED bằng nhau d) biết sđ cung BD 60 độ ,tính số đo góc ECH
Đọc tiếp
Cho nửa đường tròn tâm O, đường kính AB ,vẽ điểm S ở bên ngoài nửa đường tròn sao cho hai đoạn thẳng AS và BS cắt nửa đường tròn nói trên tại C và D .AD cắt BC tại H , hai đường thẳng AB và SH cắt nhau tại E.
a) chứng minh tứ giác ACHE nội tiếp đường tròn
b) chứng minh hai góc HED va HBD bằng nhau
c) chứng minh hai góc CEH va HED bằng nhau
d) biết sđ cung BD =60 độ ,tính số đo góc ECH
1. Từ A ngoài đường tròn tâm O. Kẻ 2 tia tiếp tuyến AM , AN. Biết góc MAN a độ ( không đổi ). Từ I bất kì trên cung nhỏ MN, vẽ tiếp tuyến cắt AM , AN tại B và C. OB và OC cắt đường tròn O tại D và E. CM : Cung DE không đổi khi I chạy trên cung MN2. Cho đường tròn O và O cắt nhau tại A và B. Qua A kẻ đường thẳng vuông góc với AB cắt đường tròn O tại C, cắt đường tròn O tại D. Tia CB cắt đường tròn O tại F , tia DB cắt đường tròn O tại E. CM : AB là tia phân giác góc EAF3. Cho tam giác ABC nhọn....
Đọc tiếp
1. Từ A ngoài đường tròn tâm O. Kẻ 2 tia tiếp tuyến AM , AN. Biết góc MAN = a độ ( không đổi ). Từ I bất kì trên cung nhỏ MN, vẽ tiếp tuyến cắt AM , AN tại B và C. OB và OC cắt đường tròn O tại D và E. CM : Cung DE không đổi khi I chạy trên cung MN
2. Cho đường tròn O và O' cắt nhau tại A và B. Qua A kẻ đường thẳng vuông góc với AB cắt đường tròn O tại C, cắt đường tròn O' tại D. Tia CB cắt đường tròn O' tại F , tia DB cắt đường tròn O tại E. CM : AB là tia phân giác góc EAF
3. Cho tam giác ABC nhọn. Điểm I bất kì trong tam giác. Kẻ IH vuông góc AB , IK vuông góc AC , IL vuông góc AB. Tìm vị trí điểm I sao cho : AL^2 + BH^2 + CK^2 đạt gtnn
1.Trên mp có 11 đường thẳng đôi 1 ko song song C/m:có 2 đường thẳng tạo với nhau 1 góc 17 độ2.Cho (O) đường kính AB.Lấy C ngoài đoạn thẳng AB (C nằm trên đường thẳng AB).Kẻ 2 tiếp tuyến CE và CF. AB cắt EF tại I, kẻ cát tuyến CMN. C/m: góc AIM góc BIN3.Cho tam giác ABC ngoại tiếp đường tròn (O).Biết D,E,F là các tiếp điểm , D thuộc AC, E thuộc AB, F thuộc BC Biết OEr, ABc, ACb, BCaC/m:a) (a+b+c)*r2S ( S là diện tích tam giác ABC)b)nếu (a+b+c)(a+b-c)4S thì tam giác ABC vuông
Đọc tiếp
1.Trên mp có 11 đường thẳng đôi 1 ko song song C/m:có 2 đường thẳng tạo với nhau 1 góc <17 độ
2.Cho (O) đường kính AB.Lấy C ngoài đoạn thẳng AB (C nằm trên đường thẳng AB).Kẻ 2 tiếp tuyến CE và CF. AB cắt EF tại I, kẻ cát tuyến CMN. C/m: góc AIM= góc BIN
3.Cho tam giác ABC ngoại tiếp đường tròn (O).Biết D,E,F là các tiếp điểm , D thuộc AC, E thuộc AB, F thuộc BC Biết OE=r, AB=c, AC=b, BC=a
C/m:a) (a+b+c)*r=2S ( S là diện tích tam giác ABC)
b)nếu (a+b+c)(a+b-c)=4S thì tam giác ABC vuông
Cho hình lập phương ABCD.A′B′C′D′ cạnh bằng a. Gọi M là trung điểm cạnh DD′ (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng CB′ và MC′ bằng A.
2
2
9
B.
10
10
C.
2
9
D.
10
5
Đọc tiếp
Cho hình lập phương ABCD.A′B′C′D′ cạnh bằng a. Gọi M là trung điểm cạnh DD′ (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng CB′ và MC′ bằng
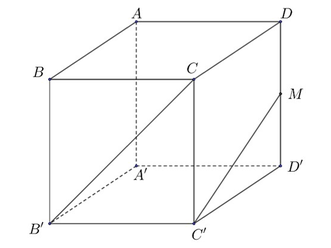
A. 2 2 9
B. 10 10
C. 2 9
D. 10 5
Cho góc xOy = 70 độ, vẽ tia phân giác Ot của góc xOy
a, Tính góc yOt
b, Trên cùng một nửa mặt phẳng bờ Ox có chứa tia Oy, vẽ tia Oz sao cho góc xOz = 90 độ, tính số đo góc yOz và viết tên 1 cặp góc phụ nhau trong hình
c, Vẽ đường tròn tâm O bán kính 3 cm. Đường tròn này cắt tia đối của tia Ox tại A. Tính OA
Cho hình lập phương ABCD.A′B′C′D′ (tham khảo hình vẽ bên). Góc giữa hai đường thẳng AC và BD′ bằng
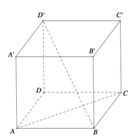
A. 90 °
B. 30 °
C. 60 °
D. 45 °
Cho hình lập phương ABCD.A′B′C′D′ (tham khảo hình vẽ bên). Góc giữa hai đường thẳng AC và BD′ bằng A.
90
°
B.
30
°
C.
60
°
D.
45
°
Đọc tiếp
Cho hình lập phương ABCD.A′B′C′D′ (tham khảo hình vẽ bên). Góc giữa hai đường thẳng AC và BD′ bằng

A. 90 °
B. 30 °
C. 60 °
D. 45 °








