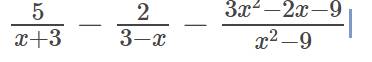Ta có:\(A=\dfrac{5}{x+3}-\dfrac{2}{3-x}-\dfrac{3x^2-2x-9}{x^2-9}\)
\(\Rightarrow A=\dfrac{5\left(x-3\right)+2\left(x+3\right)-\left(3x^2-2x-9\right)}{\left(x+3\right)\left(x-3\right)}\)
\(\Rightarrow A=\dfrac{5x-15+2x+6-3x^2+2x+9}{\left(x+3\right)\left(x-3\right)}\)
\(\Rightarrow A=\dfrac{-3x^2+9x}{\left(x+3\right)\left(x-3\right)}=\dfrac{-3x\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}=\dfrac{-3x}{x+3}\)
a,\(\left|x-2\right|=1\Rightarrow\left[{}\begin{matrix}x-2=1\\x-2=-1\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)
+, Thay \(x=3\) vào A ta được:
\(A=\dfrac{-3x}{x+3}=\dfrac{-3.3}{3+3}=\dfrac{-9}{6}=\dfrac{-3}{2}\)
+,Thay \(x=1\) vào A ta được:
\(A=\dfrac{-3x}{x+3}=\dfrac{-3.1}{1+3}=\dfrac{-3}{4}\)
b,Ta có: \(A=\dfrac{-3x}{x+3}=\dfrac{-3\left(x+3\right)+9}{x+3}=-3+\dfrac{9}{x+3}\)
Vì \(x\in Z\Rightarrow A\in Z\Rightarrow\dfrac{9}{x+3}\in Z\)
\(\Rightarrow x+3\inƯ_{\left(9\right)}\Rightarrow x+3\in\left\{1;-1;3;-3;9;-9\right\}\)
\(\Rightarrow\) Ta có bảng sau:
| \(x+3\) | \(1\) | \(-1\) | \(3\) | \(-3\) | \(9\) | \(-9\) |
| \(x\) | \(-2\) (tm) | \(-4\)(tm) | \(0\) (tm) | \(-6\)(tm) | \(6\) (tm) | \(-12\)(tm) |
Vậy \(x\in\left\{-12;-6;-4;-2;0;6\right\}\) thì A\(\in\)Z