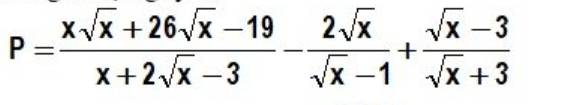Lời giải:
a. ĐKXĐ: $x\geq 0; x\neq 1$
\(P=\frac{x\sqrt{x}+26\sqrt{x}-19}{(\sqrt{x}-1)(\sqrt{x}+3)}-\frac{2\sqrt{x}(\sqrt{x}+3)}{(\sqrt{x}-1)(\sqrt{x}+3)}+\frac{(\sqrt{x}-3)(\sqrt{x}-1)}{(\sqrt{x}+3)(\sqrt{x}-1)}\)
\(=\frac{x\sqrt{x}+26\sqrt{x}-19-(2x+6\sqrt{x})+(x-4\sqrt{x}+3)}{(\sqrt{x}+3)(\sqrt{x}-1)}\\ =\frac{x\sqrt{x}+16\sqrt{x}-x-16}{(\sqrt{x}+3)(\sqrt{x}-1)}\\ =\frac{(x+16)(\sqrt{x}-1)}{(\sqrt{x}-1)(\sqrt{x}+3)}=\frac{x+16}{\sqrt{x}+3}\)
b.
$P=\frac{x+16}{\sqrt{x}+3}=\frac{(x-9)+25}{\sqrt{x}+3}$
$=(\sqrt{x}-3)+\frac{25}{\sqrt{x}+3}=(\sqrt{x}+3)+\frac{25}{\sqrt{x}+3}-6$
$\geq 2\sqrt{25}-6=4$ (áp dụng BĐT Cô-si)
Vậy $P_{\min}=4$. Giá trị này đạt tại $\sqrt{x}+3=\frac{25}{\sqrt{x}+3}\Leftrightarrow x=4$