ai giúp mình bài 2 vs =))))
Bài 5:
\(a+b+c+ab+bc+ca=6\)
-Áp dụng BĐT AM-GM ta có:
\(\dfrac{\left(a+1\right)^2}{4}+\dfrac{\left(b+1\right)^2}{4}+\dfrac{\left(c+1\right)^2}{4}+\dfrac{\left(a+b\right)^2}{4}+\dfrac{\left(b+c\right)^2}{4}+\dfrac{\left(c+a\right)^2}{4}\ge a+b+c+ab+bc+ca=6\)\(\Leftrightarrow\left(a+1\right)^2+\left(b+1\right)^2+\left(c+1\right)^2+\left(a+b\right)^2+\left(b+c\right)^2+\left(c+a\right)^2\ge24\)
\(\Leftrightarrow3\left(a^2+b^2+c^2\right)+2\left(a+b+c+ab+bc+ca\right)+3\ge24\)
\(\Leftrightarrow3\left(a^2+b^2+c^2\right)+2.6+3\ge24\)
\(\Leftrightarrow3\left(a^2+b^2+c^2\right)\ge9\)
\(\Leftrightarrow a^2+b^2+c^2\ge3\left(đpcm\right)\)
-Dấu "=" xảy ra khi \(a=b=c=1\)
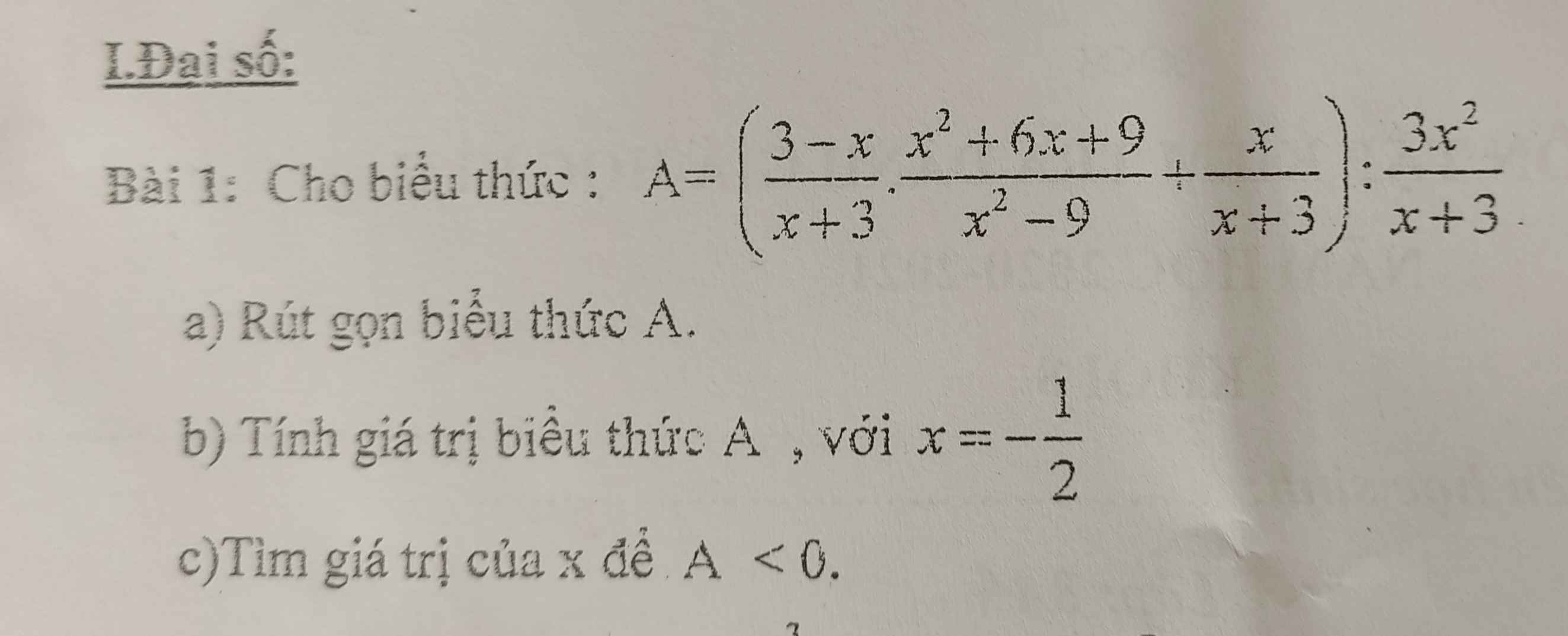
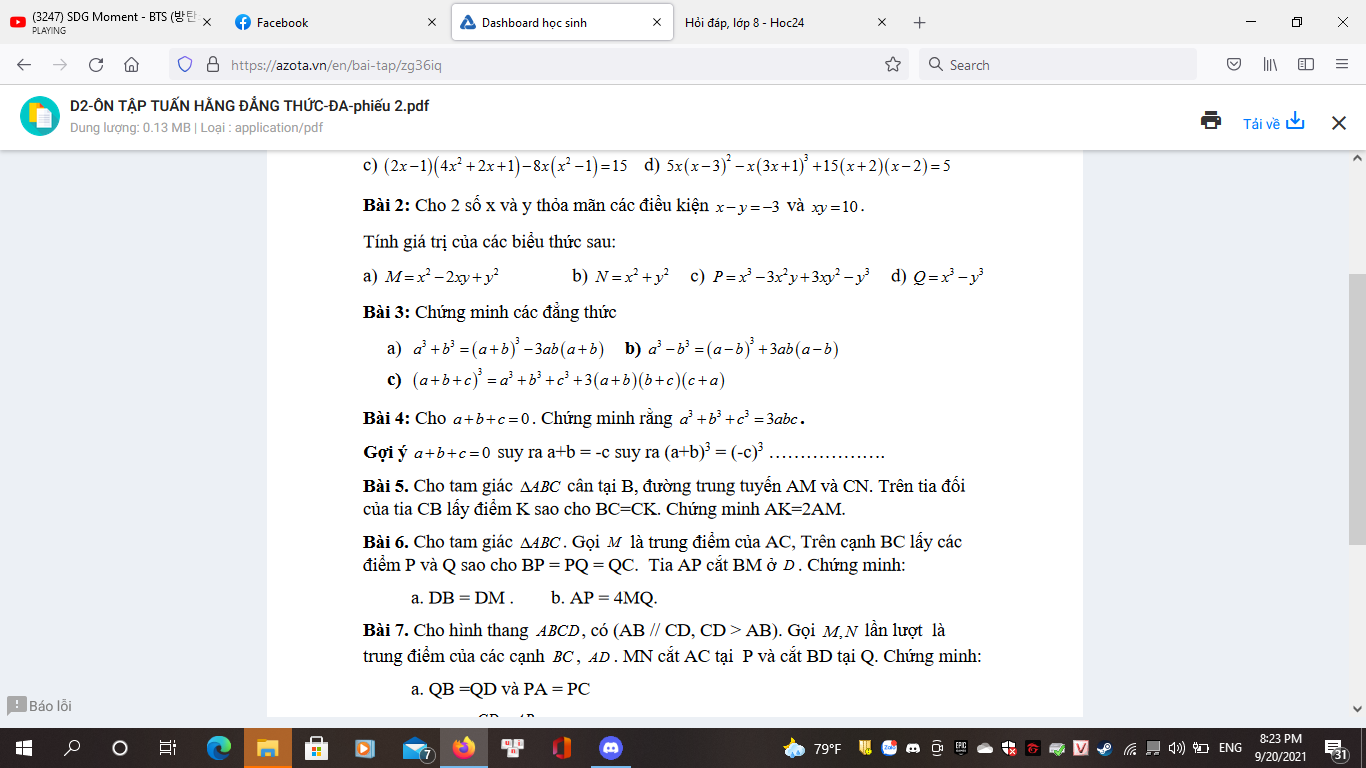mng giúp mình bài 2 bài 3 bài 4 vs ah
