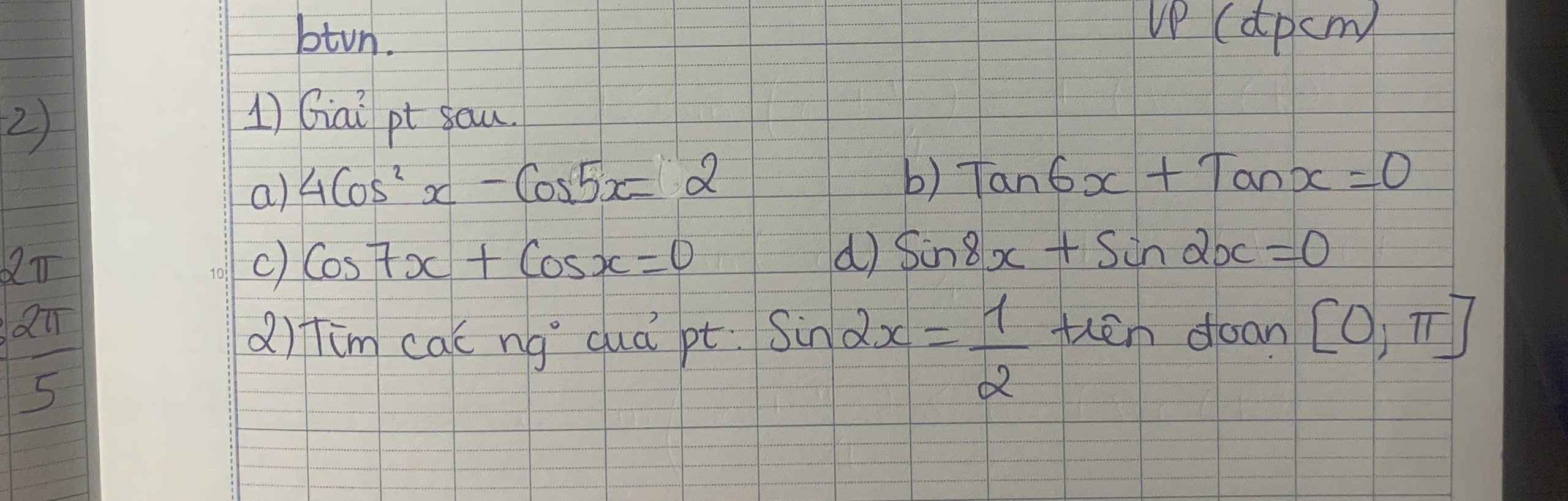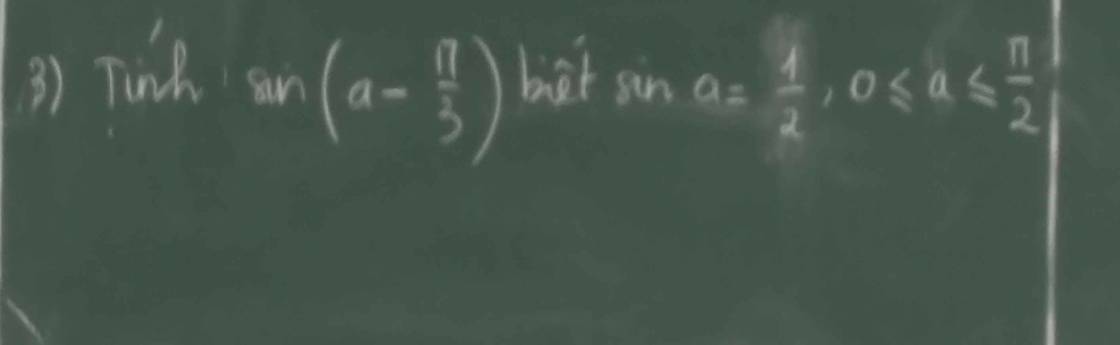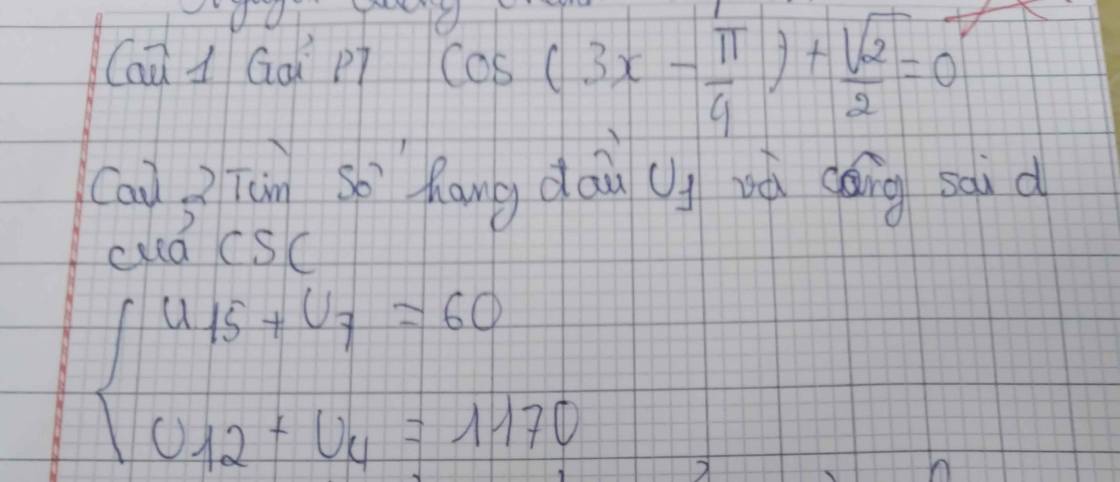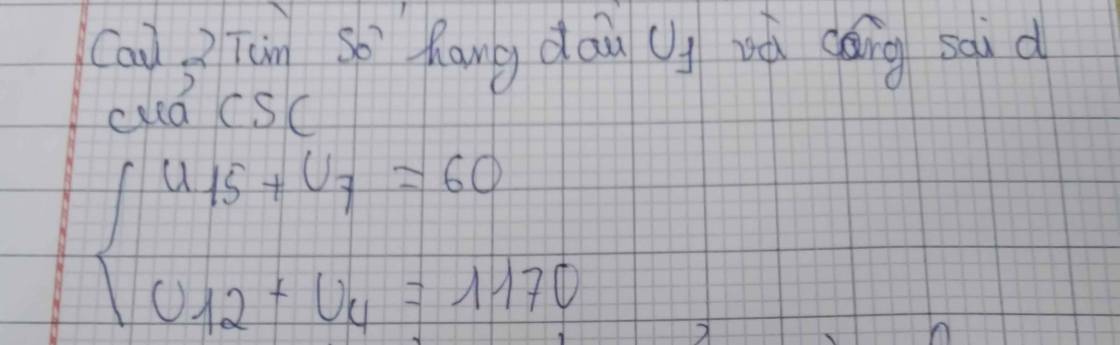Bài 1:
b: ĐKXĐ: \(\left\{{}\begin{matrix}6x\ne\dfrac{\Omega}{2}+k\Omega\\x\ne\dfrac{\Omega}{2}+k\Omega\end{matrix}\right.\Leftrightarrow x\ne\dfrac{\Omega}{12}+\dfrac{k\Omega}{6}\)
\(tan6x+tanx=0\)
=>tan 6x=-tan x=tan(-x)
=>\(6x=-x+k\Omega\)
=>\(7x=k\Omega\)
=>\(x=\dfrac{k\Omega}{7}\left(nhận\right)\)
c: \(cos7x+cosx=0\)
=>\(2\cdot cos\left(\dfrac{7x+x}{2}\right)\cdot cos\left(\dfrac{7x-x}{2}\right)=0\)
=>\(cos4x\cdot cos3x=0\)
=>\(\left[{}\begin{matrix}cos4x=0\\cos3x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}4x=\dfrac{\Omega}{2}+k\Omega\\3x=\dfrac{\Omega}{2}+k\Omega\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\Omega}{8}+\dfrac{k\Omega}{4}\\x=\dfrac{\Omega}{6}+\dfrac{k\Omega}{3}\end{matrix}\right.\)
d: sin 8x+sin 2x=0
=>sin 8x=-sin2x=sin(-2x)
=>\(\left[{}\begin{matrix}8x=-2x+k2\Omega\\8x=\Omega+2x+k2\Omega\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}10x=k2\Omega\\6x=\Omega+k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{k\Omega}{5}\\x=\dfrac{\Omega}{6}+\dfrac{k\Omega}{3}\end{matrix}\right.\)
Bài 2:
\(sin2x=\dfrac{1}{2}\)
=>\(\left[{}\begin{matrix}2x=\dfrac{\Omega}{6}+k2\Omega\\2x=\Omega-\dfrac{\Omega}{6}+k2\Omega=\dfrac{5}{6}\Omega+k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{\Omega}{12}+k\Omega\\x=\dfrac{5}{12}\Omega+k\Omega\end{matrix}\right.\)
\(x\in\left[0;\Omega\right]\)
=>\(\left[{}\begin{matrix}k\Omega+\dfrac{\Omega}{12}\in\left[0;2\Omega\right]\\k\Omega+\dfrac{5}{12}\Omega\in\left[0;2\Omega\right]\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}k+\dfrac{1}{12}\in\left[0;2\right]\\k+\dfrac{5}{12}\in\left[0;2\right]\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}k\in\left[-\dfrac{1}{12};\dfrac{23}{12}\right]\\k\in\left[-\dfrac{5}{12};\dfrac{19}{12}\right]\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}k\in\left\{0;1\right\}\\k\in\left\{0;1\right\}\end{matrix}\right.\)
=>Các nghiệm của phương trình sin 2x=1/2 trên đoạn [0;pi] là:
\(\dfrac{\Omega}{12}+0\cdot\Omega=\dfrac{\Omega}{12};\dfrac{\Omega}{12}+1\cdot\Omega=\dfrac{13}{12}\Omega;\dfrac{5}{12}\Omega;\dfrac{5}{12}\Omega+\Omega=\dfrac{17}{12}\Omega\)