`#040911`
`b)`
\(A=\dfrac{1}{1\times3}+\dfrac{1}{3\times5}+\dfrac{1}{5\times7}+...+\dfrac{1}{19\times21}\)
`=`\(\dfrac{1}{2}\times\left(\dfrac{2}{1\times3}+\dfrac{2}{3\times5}+\dfrac{2}{5\times7}+...+\dfrac{2}{19\times21}\right)\)
`=`\(\dfrac{1}{2}\times\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{19}-\dfrac{1}{21}\right)\)
`=`\(\dfrac{1}{2}\times\left(1-\dfrac{1}{21}\right)\)
\(=\dfrac{1}{2}\times\dfrac{20}{21}\\ =\dfrac{10}{21}\\ \text{ Vậy, A = }\dfrac{10}{21}\)

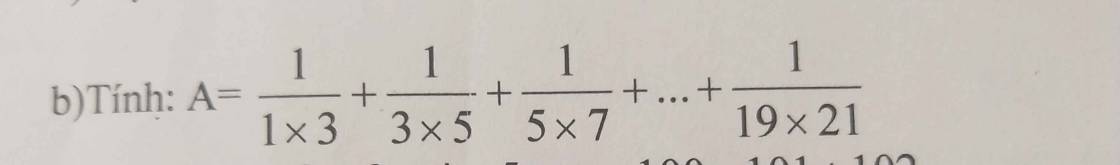




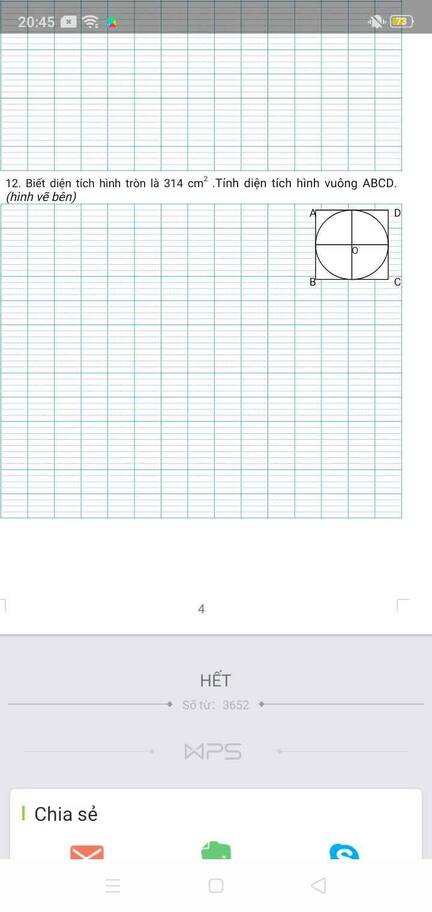










 mn giúp tớ nhé!! cảm ơn ạ
mn giúp tớ nhé!! cảm ơn ạ giúp tớ với tớ cảm ơn
giúp tớ với tớ cảm ơn