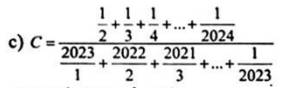\(C=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2024}}{\dfrac{2023}{1}+\dfrac{2022}{2}+...+\dfrac{1}{2023}}\)
\(=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2024}}{\left(1+\dfrac{2022}{2}\right)+\left(1+\dfrac{2021}{3}\right)+...+\left(1+\dfrac{1}{2023}\right)+1}\)
\(=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2024}}{\dfrac{2024}{2}+\dfrac{2024}{3}+...+\dfrac{2024}{2023}+\dfrac{2024}{2024}}\)
\(=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2024}}{2024\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2024}\right)}=\dfrac{1}{2024}\)