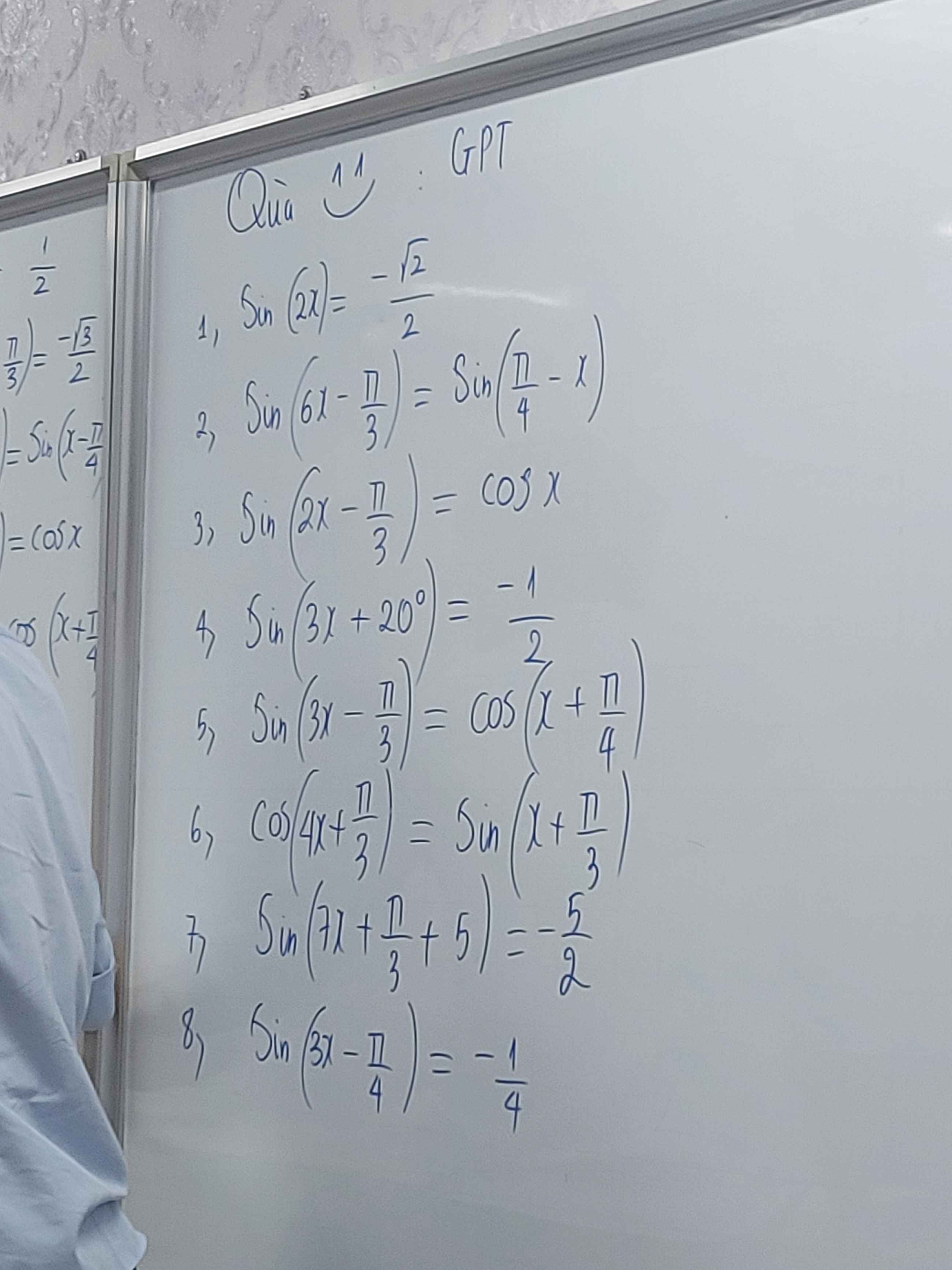`5)sin(3x-\pi/3)=cos(x+\pi/4)`
`<=>sin(3x-\pi/3)=sin(\pi/4-x)`
`<=>`$\left[\begin{matrix} 3x-\dfrac{\pi}{3}=\dfrac{\pi}{4}-x+k2\pi\\ 3x-\dfrac{\pi}{3}=\dfrac{3\pi}{4}+x+k2\pi\end{matrix}\right.$
`<=>` $\left[\begin{matrix} x=\dfrac{7\pi}{48}+\dfrac{k\pi}{2}\\ x=\dfrac{5\pi}{24}+k\pi\end{matrix}\right.$ `(k in ZZ)`
______________________________________________________
`6)cos(4x+\pi/3)=sin(x+\pi/3)`
`<=>cos(4x+\pi/3)=cos(\pi/6-x)`
`<=>` $\left[\begin{matrix} 4x+\dfrac{\pi}{3}=\dfrac{\pi}{6}-x+k2\pi\\ 4x+\dfrac{\pi}{3}=-\dfrac{\pi}{6}+x+k2\pi\end{matrix}\right.$
`<=>` $\left[\begin{matrix} x=-\dfrac{\pi}{30}+\dfrac{k2\pi}{5}\\ x=-\dfrac{\pi}{6}+\dfrac{k2\pi}{3}\end{matrix}\right.$ `(k in ZZ)`