Các câu hỏi tương tự
Cho hai hàm số: ; . Có bao nhiêu giá trị nguyên của a để mỗi hàm số có hai điểm cực trị đồng thời giữa hai điểm cực trị của hàm này có một điểm cực trị của hàm kia A. 1 B. 2 C.3 . D. 4
Đọc tiếp
Cho hai hàm số: 
; 
. Có bao nhiêu giá trị nguyên của a để mỗi hàm số có hai điểm cực trị đồng thời giữa hai điểm cực trị của hàm này có một điểm cực trị của hàm kia
A. 1
B. 2
C.3 .
D. 4
Cho hàm số y x4-2( m+1)x2+ m ( C). Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số C có ba điểm cực trị A: B; C sao cho OA BC ; trong đó O là gốc tọa độ, A là điểm cực trị thuộc trục tung, B và C là hai điểm cực trị còn lại. A.
m
2
±
2
2
B.
m
2
+
2
2
C.
m
2...
Đọc tiếp
Cho hàm số y= x4-2( m+1)x2+ m ( C). Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số C có ba điểm cực trị A: B; C sao cho OA= BC ; trong đó O là gốc tọa độ, A là điểm cực trị thuộc trục tung, B và C là hai điểm cực trị còn lại.
A. m = 2 ± 2 2
B. m = 2 + 2 2
C. m = 2 - 2 2
D. m = ± 1
Cho hàm số
y
x
4
-
2
(
m
+
1
)
x
2
+
m
(
C
)
. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số (C) có b...
Đọc tiếp
Cho hàm số y = x 4 - 2 ( m + 1 ) x 2 + m ( C ) . Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số (C) có ba điểm cực trị A, B, C sao cho OA = BC; trong đó O là gốc tọa độ, A là điểm cực trị thuộc trục tung, B và C là hai điểm cực trị còn lại
A. m = 2 ± 2 2
B. m = 2 + 2 2
C. m = 2 - 2 2
D. m = ± 1
Cho đồ thị (Cn) của hàm số
y
x
3
-
3
m
x
2
+
3
(
m
2
-
1
)
x
-
m
3
+
1
và điểm M(-2;2) Biết đồ thị (Cn)có hai điểm cực trị A,B và tam giác ABM vuông tại M. Hỏi giá trị nào của m cho dưới đây thỏa mãn bải toán A. B. C. Không có m...
Đọc tiếp
Cho đồ thị (Cn) của hàm số y = x 3 - 3 m x 2 + 3 ( m 2 - 1 ) x - m 3 + 1 và điểm M(-2;2) Biết đồ thị (Cn)có hai điểm cực trị A,B và tam giác ABM vuông tại M. Hỏi giá trị nào của m cho dưới đây thỏa mãn bải toán
A.
B. 
C. Không có m
D. Vô số giá trị m
Cho hàm số
y
x
3
+
bx
2
+
cx
+
d
biết đồ thị hàm số đã cho có hai điểm cực trị và đường thẳng nối hai điểm cực trị ấy đi qua điểm A(0; 1) .Hãy tìm giá trị nhỏ nhất của biểu thức T bcd + 2bc + 3d + 20 A. B. C. D.
Đọc tiếp
Cho hàm số y = x 3 + bx 2 + cx + d biết đồ thị hàm số đã cho có hai điểm cực trị và đường thẳng nối hai điểm cực trị ấy đi qua điểm A(0; 1) .Hãy tìm giá trị nhỏ nhất của biểu thức T= bcd + 2bc + 3d + 20
A. 
B. 
C. 
D. 
Cho
a
,
b
,
c
∈
R
sao cho hàm số
y
x
3
+
a
x
2
+
b
x
+
c
đạt cực trị tại x 3, đồng thời có
y
(
0
)
3
và
y
3...
Đọc tiếp
Cho a , b , c ∈ R sao cho hàm số y = x 3 + a x 2 + b x + c đạt cực trị tại x = 3, đồng thời có y ( 0 ) = 3 và y 3 = 3 . Hỏi trong không gian Oxyz, điểm M ( a , b , c ) nằm trong mặt cầu nào sau đây?
Biết phương trình
a
x
3
+
b
x
2
+
c
x
+
d
0
a
≠
0
có đúng hai nghiệm thực. Hỏi đồ thị hàm số
y
a
x
3
+
b
x
2
+
c...
Đọc tiếp
Biết phương trình a x 3 + b x 2 + c x + d = 0 a ≠ 0 có đúng hai nghiệm thực. Hỏi đồ thị hàm số y = a x 3 + b x 2 + c x + d có bao nhiêu điểm cực trị?
A. 4
B. 5
C. 6
D. 3
Cho hàm số
y
f
x
có bảng biến thiên như hình vẽ. Hỏi hàm số có bao nhiêu điểm cực trị?
Đọc tiếp
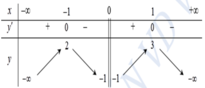
Cho hàm số y = f x có bảng biến thiên như hình vẽ. Hỏi hàm số có bao nhiêu điểm cực trị?
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ. Hỏi hàm số có bao nhiêu điểm cực trị?
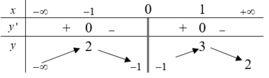
A. Có một điểm
B. Có ba điểm
C. Có hai điểm
D. Có bốn điểm
Tìm giá trị thực của tham số m để đồ thị hàm số
y
x
3
-
3
m
x
2
+
2
có hai điểm cực trị là A và B sao cho A, B và điểm M(1;-2) thẳng hàng.
Đọc tiếp
Tìm giá trị thực của tham số m để đồ thị hàm số y = x 3 - 3 m x 2 + 2 có hai điểm cực trị là A và B sao cho A, B và điểm M(1;-2) thẳng hàng.
