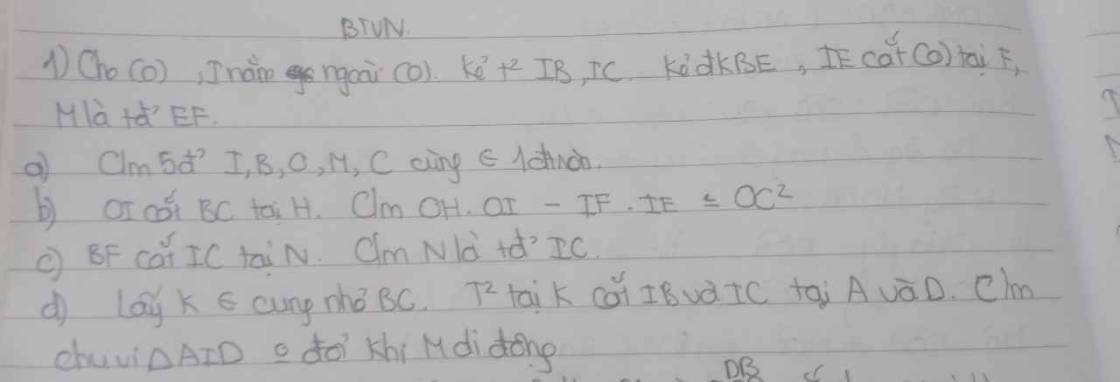\(\frac{6a+1}{3a-1}=2+\frac{3}{3a-1}\)
Để (6a + 1) chia hết cho (3a - 1) thì (3a - 1) \(\in\) Ư(3) = {1;-1;3;-3}
3a - 1 = 1 => 3a = 2 => a = 2/3 (loại)
3a - 1 = -1 => 3a = 0 => a = 0 (nhận)
3a - 1 = 3 => 3a = 4 => a = 4/3 (loại)
3a - 1 =-3 => 3a = -2 => a = -2/3 (loại)
Vậy a = 0
ta se co :
(6a - 2 ) + 3 chia het cho 3a - 1
2.(3a - 1) + 3 chia het cho 3a - 1
vi 2. (3a - 1) chia het cho 3a - 1
nen 3 chia het cho 3a - 1
3a - 1 \(\in\)U (3)= { -3;-1;1;3}
vi 3a - 1 la so chia 3 du 2 nen ta co :
3a - 1 = -1 \(\Rightarrow\)3a = -1+1= 0 \(\Rightarrow\)a = 0 : 3 = 0
vay a = 0
cho minh nha ban , thanks
4 : 3 = tứ tam = tám tư = 8 : 4 = 2
Đ/S : .....
4:3=1,333333333333333333333333333333333333333333333............v.v các số 3










 Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn



 Gi
Gi