1,Cho hbh ABCD có BC=2AB,góc B = 60°.Gọi M,N lần lượt là trung điểm của AD và BC.Gọi I là điểm đối xứng của B qua A .Vẽ hình
a,Tứ giác AMNB là hình j?Vì sao
b,Cminh:AN Vuông góc với ND
c,T/g ACDI là hình j?Vì sao
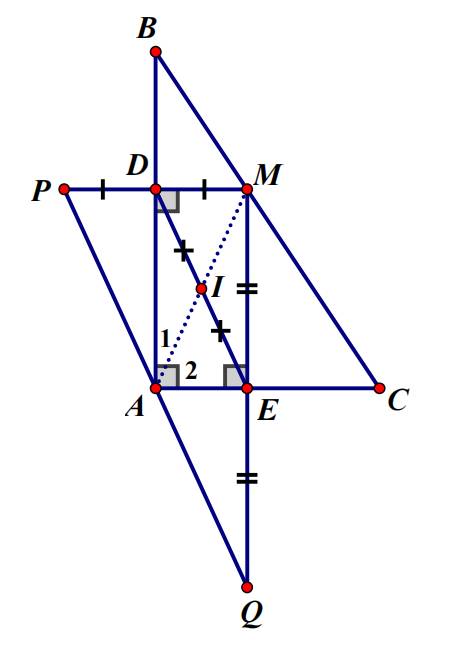
2,Cho▲ABC vuông tại A,M là tđ của BC.kẻ MD vuông góc AB (D thuộc AB),ME vuông góc AC (E thuộc AC). Vẽ hình
a,T/g ADME là hìng j?Vì sao
b▲ABC có điều kiện j thì t/g ADME là hình vuông
3,Phân tích đa thức
ab(a+b)-bc(b+c)-ac(c-a)
2:
a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{DAE}=90^0\)
=>ADME là hình chữ nhật
b: Hình chữ nhật ADME trở thành hình vuông khi AM là phân giác của góc BAC
Xét ΔABC có
AM là đường trung tuyến
AM là đường phân giác
Do đó: ΔABC cân tại A
=>AB=AC
3:
\(ab\left(a+b\right)-bc\left(b+c\right)-ac\left(c-a\right)\)
\(=a^2b+ab^2-b^2c-bc^2+ac\left(a-c\right)\)
\(=\left(a^2b-bc^2\right)+\left(ab^2-b^2c\right)+ac\left(a-c\right)\)
\(=b\left(a^2-c^2\right)+b^2\left(a-c\right)+ac\left(a-c\right)\)
\(=b\left(a-c\right)\left(a+c\right)+\left(a-c\right)\left(b^2+ac\right)\)
\(=\left(a-c\right)\left(ba+bc+b^2+ac\right)\)
\(=\left(a-c\right)\left[\left(ba+b^2\right)+\left(bc+ac\right)\right]\)
\(=\left(a-c\right)\left[b\left(a+b\right)+c\left(a+b\right)\right]\)
1:
a: Ta có: ABCD là hình bình hành
=>AD=BC(1)
Ta có: M là trung điểm của AD
=>\(MA=MD=\dfrac{AD}{2}\left(2\right)\)
Ta có:N là trung điểm của BC
=>\(NB=NC=\dfrac{BC}{2}\)(3)
Từ (1),(2),(3) suy ra AM=MD=CN=NB
Xét tứ giác AMNB có
AM//NB
AM=NB
Do đó: AMNB là hình bình hành
Hình bình hành AMNB có AM=AB(=AD/2)
nên AMNB là hình thoi
b: Ta có: AMNB là hình thoi
=>MN=AM
mà \(AM=\dfrac{AD}{2}\)
nên \(NM=\dfrac{AD}{2}\)
Xét ΔNAD có
NM là đường trung tuyến
\(NM=\dfrac{AD}{2}\)
Do đó: ΔNAD vuông tại N
=>AN\(\perp\)ND
c:
Ta có: AB=DC
AB=AI
Do đó: DC=AI
Ta có: AB//DC
I\(\in\)AB
Do đó: IA//DC
Xét ΔABN có BA=BN(=BC/2) và \(\widehat{B}=60^0\)
nên ΔBAN đều
=>\(AN=BN=\dfrac{BC}{2}\)
Xét ΔBAC có
AN là đường trung tuyến
\(AN=\dfrac{BC}{2}\)
Do đó: ΔBAC vuông tại A
=>BA\(\perp\)AC
=>CA\(\perp\)AI
Xét tứ giác AIDC có
AI//DC
AI=DC
Do đó: AIDC là hình bình hành
Hình bình hành AIDC có \(\widehat{IAC}=90^0\)
nên AIDC là hình chữ nhật