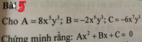\(\left|x\right|+x=\dfrac{1}{3}\)
\(\Rightarrow\left|x\right|=\dfrac{1}{3}-x\)
\(\left|x\right|=\left\{{}\begin{matrix}xkhix\ge0\\-xkhix< 0\end{matrix}\right.\)
Với \(x\ge0\Rightarrow x=\dfrac{1}{3}-x\Rightarrow2x=\dfrac{1}{3}\Rightarrow x=\dfrac{1}{6}\left(tm\right)\)
Với \(x< 0\Rightarrow-x=\dfrac{1}{3}-x\Rightarrow-x+x=\dfrac{1}{3}\Rightarrow0=\dfrac{1}{3}\left(VL\right)\)
Vậy \(x=\dfrac{1}{6}\)
\(\left|x\right|+x=\dfrac{1}{3}\left(1\right)\)
TH1 : \(x\ge0\)
\(\left(1\right)=>x+x=\dfrac{1}{3}\\ =>2x=\dfrac{1}{3}\\ =>x=\dfrac{1}{3}:2=\dfrac{1}{6}\left(TMDK\right)\)
\(TH2:x< 0\)
\(\left(1\right)=>-x+x=\dfrac{1}{3}\\ =>0=\dfrac{1}{3}\)( Vô lí )
Vậy `x=1/6`