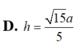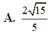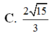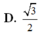Question

1. Trong không gian có 3 điểm A(1;-2;4) B(3;1;2) C(0;1;1) a, tính vecto AB;BC suy ra độ dài cạnh AB,và BC b, viết phương trình mặt phẳng ABC c, tính khoảng cách từ điểm M(2;1;3) đến mặt phẳng (ABC)

Answer 1

\(\overrightarrow{AB}=\left(2;3;2\right)\Rightarrow AB=\sqrt{2^2+3^2+2^2}=\sqrt{17}\)

\(\overrightarrow{BC}=\left(-3;0;-1\right)\Rightarrow BC=\sqrt{\left(-3\right)^2+0^2+\left(-1\right)^2}=\sqrt{10}\)

\(\left[\overrightarrow{AB};\overrightarrow{BC}\right]=\left(-3;-4;9\right)\)

Mặt phẳng (ABC) nhận (-3;-4;9) là 1 vtpt

Phương trình (ABC):

\(-3\left(x-1\right)-4\left(y+2\right)+9\left(z-4\right)=0\)

\(\Leftrightarrow-3x-4y+9z-41=0\)

\(d\left(M;\left(ABC\right)\right)=\dfrac{\left|-3.2+4.1+9.3-41\right|}{\sqrt{\left(-3\right)^2+\left(-4\right)^2+9^2}}=\dfrac{8\sqrt{106}}{53}\)