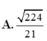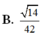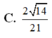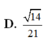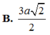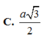1. cho tứ diện ABCD có AB=AC=AD và \(\stackrel\frown{BAC}=\stackrel\frown{BAD}\)=60 độ. Hãy xác định góc giữa 2 vecto \(\overrightarrow{AB}\) và \(\overrightarrow{CD}\)
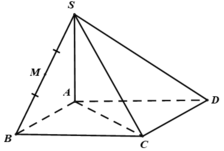
2. cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a và các cạnh bên đều bằng a. Gọi M và N lần lượt là trung điểm AD và SD. Số đo của góc \(\left(\overrightarrow{MN},\overrightarrow{SC}\right)\) bằng
1.
Do \(AB=AC=AD\) và \(\widehat{BAC}=\widehat{BAD}=60^0\)
\(\Rightarrow\) Các tam giác ABC và ABD là các tam giác đều (tam giác cân có 1 góc 60 độ)
\(\Rightarrow AB=AC=AD=BC=BD\)
\(\Rightarrow\Delta BCD\) cân tại B
Gọi M là trung điểm CD \(\Rightarrow CD\perp BM\)
Cũng do tam giác ACD cân tại A \(\Rightarrow CD\perp AM\)
\(\Rightarrow CD\perp\left(ABM\right)\Rightarrow CD\perp AB\)
Góc giữa 2 vecto đã cho bằng 90 độ
2.
Từ giả thiết suy ra MN là đường trung bình tam giác SAD
\(\Rightarrow MN||SA\)
\(\Rightarrow\left(\overrightarrow{MN};\overrightarrow{SC}\right)=\left(\overrightarrow{AS};\overrightarrow{SC}\right)=180^0-\left(\overrightarrow{SA};\overrightarrow{SC}\right)\)
\(SA=SC=a;\)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(\Rightarrow SA^2+SC^2=AC^2\Rightarrow\left(\overrightarrow{SA};\overrightarrow{SC}\right)=90^0\)
\(\Rightarrow\left(\overrightarrow{MN};\overrightarrow{SC}\right)=90^0\)