1. △ABC vuông tại A. Trên BC lấy D sao cho BD = BA. Qua D kẻ đường thẳng vuông góc với BC cắt AC tại E.
a) C/m AE = DE
b) Đường phân giác góc ngoài tại C cắt BE tại K. Tính \(\widehat{BAK}\)
2. C/m rằng nếu tam giác vuông có 1 cạnh góc vuông bằng nửa cạnh huyền thì góc đối diện với cạnh đó bằng 30o
3. C/m rằng nếu tam giác vuông có 1 góc bằng 30o thì cạnh đối diện với góc đó bằng nửa cạnh huyền.
Câu 3:
Tam giác ABC có góc ACB = 30o => góc CAB = 60o ( do tổng 3 góc trong tam giác)
Gọi M là trung điểm của cạnh AC => MA = MC = \(\frac{BC}{2}\)
Trong tam giác vuông, đường trung tuyến xuất phát từ đỉnh góc vuông bằng \(\frac{1}{2}\)
=> AM = \(\frac{1}{2}\) AC = MB.
Xét tam giác ABM có AM = MB =>tam giác ABM là tam giác cân , mà góc MAB = 60o
=> Tam giác ABM là tam giác đều ( tam giác cân có 1 góc = 60o là tam giác đều)
<=> MA = MC = AB = \(\frac{1}{2}\)AC.
=>ĐPCM.
HÌNH VẼ
2 và 3 bạn tham khảo ở:
Câu hỏi của Doma Umaru - Toán lớp 7 - Học toán với OnlineMath
Haiz...mới tham gia trận chiến nhanh tay bên sử nên hơi mệt,vào box sử mà coi,mệt thắt gan thắt ruột
Tự vẽ hình
Câu 1:
a) ΔABE và ΔDBE có:
AB = DB (gt)
\(\widehat{BAE}=\widehat{BDE}=90^o\)
Cạnh BE chung
=> ΔABE = ΔDBE (ch.cgv)
=> AE = DE
b) Từ K kẻ KM ⊥ AB; KN ⊥ AC; KP ⊥ BC
Vì ΔABE = ΔDBE (cmt)
=> \(\widehat{ABE}=\widehat{CBE}\)
=> BE là tia phân giác của \(\widehat{ABC}\) => KM = KP (1)
Vì CK là tia phân giác của \(\widehat{NCP}\) => KN = KP (2)
Từ (1) và (2) => KM = KN
Mà AMKN là hcn (\(\widehat{AMK}=\widehat{MKN}=\widehat{KNA}=\widehat{NAM}=90^o\))
=> AMKN là hình vuông
=> \(\widehat{NAK}=\widehat{KAM}=\frac{1}{2}\widehat{NAM}=45^o\)
\(\widehat{BAK}=\widehat{BAC}+\widehat{NAK}=90^o+45^o=135^o\)
2.
Trên tia đối của tia AC lấy điểm D sao cho AC = AD.
Xét 2 \(\Delta\) vuông \(ABC\) và \(ABD\) có:
\(\widehat{BAC}=\widehat{BAD}=90^0\)
\(AC=AD\) (do cách vẽ)
Cạnh AB chung
=> \(\Delta ABC=\Delta ABD\) (2 cạnh góc vuông tương ứng bằng nhau).
=> \(BC=BD\) (2 cạnh tương ứng).
=> \(\widehat{ABC}=\widehat{ABD}\) (2 góc tương ứng).
Ta có: \(AC=\frac{1}{2}BC\left(gt\right)\)
Mà \(AC=AD\) (do cách vẽ)
=> \(AD=\frac{1}{2}BC.\)
=> \(AD+AC=BC\)
=> \(DC=BC.\)
Mà \(BC=BD\left(cmt\right)\)
=> \(BD=DC=BC.\)
=> \(\Delta BDC\) là tam giác đều.
=> \(\widehat{DBC}=60^0\) (tính chất tam giác đều).
Lại có: \(\widehat{ABC}+\widehat{ABD}=\widehat{DBC}\)
Mà \(\widehat{ABC}=\widehat{ABD}\left(cmt\right)\)
=> \(\widehat{ABC}=\widehat{ABD}=\frac{\widehat{DBC}}{2}\)
=> \(\widehat{ABC}=\widehat{ABD}=\frac{60^0}{2}=30^0.\)
=> \(\widehat{ABC}=30^0\left(đpcm\right).\)
Vậy nếu một tam giác vuông có 1 cạnh góc vuông bằng nửa cạnh huyền thì góc đối diện với cạnh đó bằng 30o
Chúc bạn học tốt!
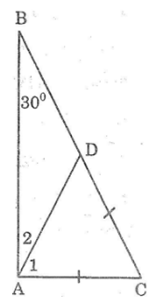
3.
Xét \(\Delta ABC\) có:
\(\left\{{}\begin{matrix}\widehat{A}=90^0\left(gt\right)\\\widehat{B}=30^0\left(gt\right)\end{matrix}\right.\)
Trên cạnh \(BC\) lấy điểm D sao cho \(CD=AC.\)
=> \(\Delta ACD\) cân tại C.
Vì \(\Delta ABC\) vuông tại \(A\left(gt\right)\)
=> \(\widehat{B}+\widehat{C}=90^0\) (tính chất tam giác vuông).
=> \(30^0+\widehat{C}=90^0\)
=> \(\widehat{C}=90^0-30^0\)
=> \(\widehat{C}=60^0.\)
Mà \(\Delta ACD\) cân tại \(C\left(cmt\right)\)
=> \(\Delta ACD\) đều.
=> \(\left\{{}\begin{matrix}AC=AD=CD\\\widehat{A_1}=60^0\end{matrix}\right.\) (tính chất tam giác đều).
Lại có: \(\widehat{A_1}+\widehat{A_2}=\widehat{BAC}\)
=> \(60^0+\widehat{A_2}=90^0\)
=> \(\widehat{A_2}=90^0-60^0\)
=> \(\widehat{A_2}=30^0.\)
Mà \(\widehat{B}=30^0\left(gt\right)\)
=> \(\widehat{A_2}=\widehat{B}=30^0.\)
=> \(\Delta ADB\) cân tại D.
=> \(AD=DB\) (tính chất tam giác cân).
Mà \(AC=AD=CD\left(cmt\right)\)
=> \(AC=CD=DB.\)
Mà \(CD+DB=BC.\)
=> \(CD=DB=\frac{1}{2}BC\)
Hay \(AC=CD=DB=\frac{1}{2}BC.\)
=> \(AC=\frac{1}{2}BC\left(đpcm\right).\)
Vậy nếu tam giác vuông có 1 góc bằng 30o thì cạnh đối diện với góc đó bằng nửa cạnh huyền.
Chúc bạn học tốt!
Chưa kịp làm đã trả lời hết rồi