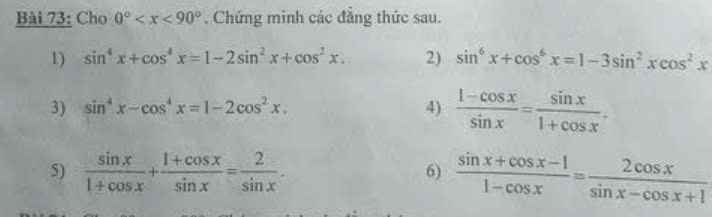1: \(sin^4x+cos^4x\)
\(=\left(sin^2x+cos^2x\right)^2-2\cdot sin^2x\cdot cos^2x\)
\(=1-2\cdot sin^2x\cdot cos^2x\)
2: \(sin^6x+cos^6x\)
\(=\left(sin^2x+cos^2x\right)^3-3\cdot sin^2x\cdot cos^2x\left(sin^2x+cos^2x\right)\)
\(=1-3\cdot sin^2x\cdot cos^2x\)
3: \(sin^4x-cos^4x\)
\(=\left(sin^2x-cos^2x\right)\left(sin^2x+cos^2x\right)\)
\(=sin^2x-cos^2x\)
\(=1-cos^2x-cos^2x=1-2\cdot cos^2x\)
4: \(\left(1-cosx\right)\left(1+cosx\right)-sin^2x\)
\(=1-cos^2x-sin^2x\)
=1-1
=0
=>\(\left(1-cosx\right)\left(1+cosx\right)=sin^2x\)
=>\(\dfrac{1-cosx}{sinx}=\dfrac{sinx}{1+cosx}\)
5: \(\dfrac{sinx}{1+cosx}+\dfrac{1+cosx}{sinx}\)
\(=\dfrac{sin^2x+\left(1+cosx\right)^2}{sinx\left(1+cosx\right)}\)
\(=\dfrac{sin^2x+cos^2x+2\cdot cosx+1}{sinx\left(1+cosx\right)}\)
\(=\dfrac{2\cdot cosx+2}{sinx\left(1+cosx\right)}=\dfrac{2}{sinx}\)
6: \(\left(sinx+cosx-1\right)\left(sinx-cosx+1\right)-2\cdot cosx\left(1-cosx\right)\)
\(=sin^2x-\left(cosx-1\right)^2-2cosx+2\cdot cos^2x\)
\(=sin^2x-\left(cos^2x-2\cdot cosx+1\right)-2\cdot cosx+2\cdot cos^2x\)
\(=sin^2x-cos^2x+2\cdot cosx-1-2\cdot cosx+2\cdot cos^2x\)
\(=sin^2x+cos^2x-1=1-1=0\)
=>\(\left(sinx+cosx-1\right)\left(sinx-cosx+1\right)=2\cdot cosx\left(1-cosx\right)\)
=>\(\dfrac{sinx+cosx-1}{1-cosx}=\dfrac{2cosx}{sinx-cosx+1}\)
1) Ta có: \(sin^2x+cos^2x=1\Leftrightarrow\left(sin^2x+cos^2x\right)^2=1\)
\(\Leftrightarrow sin^4x+2sin^2x\cdot cos^2x+cos^4x=1\)
\(\Leftrightarrow sin^4x+cos^4x=1-2sin^2x\cdot cos^2x\)
P/s: Chắc là thừa mất dấu (+) ở vế phải chứ nếu nó có (+) thì ko đúng
2) Ta có: \(sin^2x+cos^2x=1\Leftrightarrow\left(sin^2x+cos^2x\right)^3=1\)
\(\Leftrightarrow sin^6x+cos^6x+3sin^2x\cdot cos^2x\left(sin^2x+cos^2x\right)=1\)
\(\Leftrightarrow sin^6x+cos^6x=1-3sin^2x\cdot cos^2x\)
3) Ta có: \(sin^4-cos^4x=sin^4x+cos^4x-2cos^4x\)
\(=1-2sin^2x\cdot cos^2x-2cos^4x\) (theo p1)
\(=1-2cos^2x\left(sin^2x+cos^2x\right)\)
\(=1-2cos^2x\)
4) Ta có: \(\dfrac{1-cosx}{sinx}=\dfrac{\left(1-cosx\right)\left(1+cosx\right)}{sinx\left(1+cosx\right)}=\dfrac{1-cos^2x}{sinx\left(1+cosx\right)}=\dfrac{sin^2x}{sinx\left(1+cosx\right)}=\dfrac{sinx}{1+cosx}\)5) Ta có:
\(\dfrac{sinx}{1+cosx}+\dfrac{1+cosx}{sinx}=\dfrac{sin^2x+\left(1+cosx\right)^2}{sinx\left(1+cosx\right)}\)
\(=\dfrac{sin^2x+cos^2x+1+2cosx}{sinx\left(1+cosx\right)}\)
\(=\dfrac{2\left(1+cosx\right)}{sinx\left(1+cosx\right)}=\dfrac{2}{sinx}\)
6) \(\dfrac{sinx+cosx-1}{1-cosx}=\dfrac{\left(sinx+cosx-1\right)\left(sinx+cosx+1\right)}{\left(1-cosx\right)\left(sinx+cosx+1\right)}\)
\(=\dfrac{\left(sinx+cosx\right)^2-1}{sinx+cosx+1-sinx\cdot cosx-cos^2x-cosx}\)
\(=\dfrac{sin^2x+cos^2x+2sinx\cdot cosx-1}{sinx+sin^2x+cos^2x-sinx\cdot cosx-cos^2x}\)
\(=\dfrac{2sinx\cdot cosx}{sinx\left(sinx-cosx+1\right)}\)
\(=\dfrac{2cosx}{sinx-cosx+1}\)