\(\dfrac{11}{12}+\dfrac{19}{20}+\dfrac{29}{30}+...+\dfrac{109}{110}\)
\(=1-\dfrac{1}{12}+1-\dfrac{1}{20}+1-\dfrac{1}{30}+...+1-\dfrac{1}{110}\)
\(=8-\left(\dfrac{1}{12}+\dfrac{1}{20}+...+\dfrac{1}{110}\right)\)
\(=8-\left(\dfrac{1}{3\times4}+\dfrac{1}{4\times5}+...+\dfrac{1}{10\times11}\right)\)
\(=8-\left(\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{10}-\dfrac{1}{11}\right)\)
\(=8-\left(\dfrac{1}{3}-\dfrac{1}{11}\right)=8-\dfrac{8}{33}=\dfrac{256}{33}\)
\(\left(1-\dfrac{1}{2}\right)\times\left(1-\dfrac{1}{3}\right)\times...\times\left(1-\dfrac{1}{2011}\right)\)
\(=\dfrac{1}{2}\times\dfrac{2}{3}\times...\times\dfrac{2010}{2011}\)
\(=\dfrac{1}{2011}\)
\(M=\dfrac{3}{1\times3}+\dfrac{3}{3\times5}+...+\dfrac{3}{21\times23}\)
\(=\dfrac{3}{2}\times\left(\dfrac{2}{1\times3}+\dfrac{2}{3\times5}+...+\dfrac{2}{21\times23}\right)\)
\(=\dfrac{3}{2}\times\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{21}-\dfrac{1}{23}\right)\)
\(=\dfrac{3}{2}\times\left(1-\dfrac{1}{23}\right)=\dfrac{3}{2}\times\dfrac{22}{23}=\dfrac{33}{23}\)

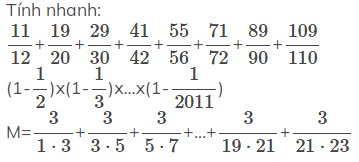








 4 và 5
4 và 5



