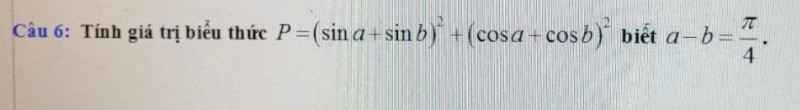Ta có:
\(\sin a+\sin b=2\sin\left(\dfrac{a+b}{2}\right).\cos\left(\dfrac{a-b}{2}\right)\)
\(\cos a+\cos b=2\cos\left(\dfrac{a+b}{2}\right).\cos\left(\dfrac{a-b}{2}\right)\)
\(\Rightarrow P=4\sin^2\left(\dfrac{a+b}{2}\right).\cos^2\left(\dfrac{a-b}{2}\right)+4\cos^2\left(\dfrac{a+b}{2}\right).\cos^2\left(\dfrac{a-b}{2}\right)\)
\(\Rightarrow P=4\cos^2\left(\dfrac{a-b}{2}\right)\left[\sin^2\left(\dfrac{a+b}{2}\right)+\cos^2\left(\dfrac{a+b}{2}\right)\right]\)
\(\Rightarrow P=4\cos^2\left(\dfrac{a-b}{2}\right)\)
\(\Rightarrow P=4\cos^2.\dfrac{\pi}{8}\)
\(\Rightarrow P=2\left[\left(2\cos^2.\dfrac{\pi}{8}-1\right)+1\right]\)
\(\Rightarrow P=2\left[\cos2.\dfrac{\pi}{8}+1\right]\)
\(\Rightarrow P=2+\sqrt{2}\)