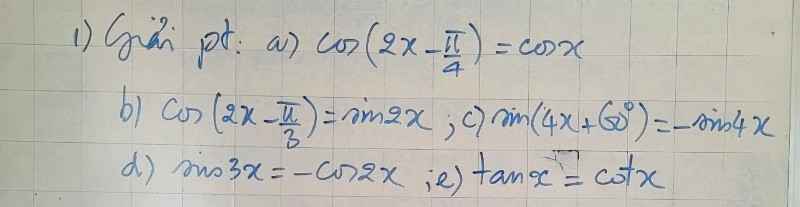a, \(cos\left(2x-\dfrac{\pi}{4}\right)=cosx\Rightarrow\left[{}\begin{matrix}2x-\dfrac{\pi}{4}=x+k2\pi\\2x-\dfrac{\pi}{4}=-x+k2\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k2\pi\\x=\dfrac{\pi}{12}+\dfrac{k2\pi}{3}\end{matrix}\right.\)
b, \(cos\left(2x-\dfrac{\pi}{3}\right)=sin2x=cos\left(\dfrac{\pi}{2}-2x\right)\Rightarrow\left[{}\begin{matrix}2x-\dfrac{\pi}{3}=\dfrac{\pi}{2}-2x+k2\pi\\2x-\dfrac{\pi}{3}=-\dfrac{\pi}{2}+2x+k2\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}4x=\dfrac{5\pi}{6}+k2\pi\\loai\end{matrix}\right.\Rightarrow x=\dfrac{5\pi}{24}+\dfrac{k\pi}{2}\)
c, \(sin\left(4x+60^0\right)=-sin4x=sin\left(-4x\right)\Rightarrow\left[{}\begin{matrix}4x+60^0=-4x+k360^0\\4x+60^0=-4x+180^0+k360^0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=7,5^0+k45^0\\x=15^0+k45^0\end{matrix}\right.\)
d, \(sin3x=-cos2x\Leftrightarrow sin3x=cos\left(\pi-2x\right)\Leftrightarrow cos\left(\dfrac{\pi}{2}-3x\right)=cos\left(\pi-2x\right)\)
\(\left[{}\begin{matrix}\dfrac{\pi}{2}-3x=\pi-2x+k2\pi\\\dfrac{\pi}{2}-3x=2x-\pi+k2\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}-x=\dfrac{1}{2}\pi+k2\pi\\-5x=-\dfrac{3}{2}\pi+k2\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{2}-k2\pi\\x=\dfrac{3}{10}\pi-\dfrac{k2\pi}{5}\end{matrix}\right.\)
e, \(tanx=cotx=tan\left(\dfrac{\pi}{2}-x\right)\Rightarrow x=\dfrac{\pi}{2}-x+k\pi\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
a: \(cos\left(2x-\dfrac{\Omega}{4}\right)=cosx\)
=>\(\left[{}\begin{matrix}2x-\dfrac{\Omega}{4}=x+k2\Omega\\2x-\dfrac{\Omega}{4}=-x+k2\Omega\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\Omega}{4}+k2\Omega\\3x=\dfrac{\Omega}{4}+k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{\Omega}{4}+k2\Omega\\x=\dfrac{\Omega}{12}+\dfrac{k2\Omega}{3}\end{matrix}\right.\Leftrightarrow x=\dfrac{\Omega}{12}+\dfrac{k2\Omega}{3}\)
b: \(cos\left(2x-\dfrac{\Omega}{3}\right)=sin2x\)
=>\(cos\left(2x-\dfrac{\Omega}{3}\right)=cos\left(\dfrac{\Omega}{2}-2x\right)\)
=>\(\left[{}\begin{matrix}2x-\dfrac{\Omega}{3}=\dfrac{\Omega}{2}-2x+k2\Omega\\2x-\dfrac{\Omega}{3}=2x-\dfrac{\Omega}{2}+k2\Omega\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}4x=\dfrac{5}{6}\Omega+k2\Omega\\-\dfrac{\Omega}{3}+\dfrac{\Omega}{2}=k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{5}{24}\Omega+\dfrac{k\Omega}{2}\\\dfrac{\Omega}{6}=k2\Omega\end{matrix}\right.\Leftrightarrow x=\dfrac{5}{24}\Omega+\dfrac{k\Omega}{2}\)
c: \(sin\left(4x+60^0\right)=-sin4x=sin\left(-4x\right)\)
=>\(\left[{}\begin{matrix}4x+60^0=-4x+k\cdot360^0\\4x+60^0=180^0+4x+k\cdot360^0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}8x=-60^0+k\cdot360^0\\k\cdot360^0=120^0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-7,5^0+k\cdot45^0\\k=\dfrac{1}{3}\left(loại\right)\end{matrix}\right.\)
Vậy: \(x=-7,5^0+k\cdot45^0\)
d: \(sin3x=-cos\left(2x\right)\)
=>cos2x=-sin3x=sin(-3x)
=>\(cos2x=cos\left(\dfrac{\Omega}{2}+3x\right)\)
=>\(\left[{}\begin{matrix}2x=\dfrac{\Omega}{2}+3x+k2\Omega\\2x=-\dfrac{\Omega}{2}-3x+k2\Omega\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}-x=\dfrac{\Omega}{2}+k2\Omega\\5x=-\dfrac{\Omega}{2}+k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=-\dfrac{\Omega}{2}-k2\Omega\\x=-\dfrac{\Omega}{10}+\dfrac{k2\Omega}{5}\end{matrix}\right.\)
e:
ĐKXĐ: \(x\ne\dfrac{\Omega}{2}+k\Omega;x\ne k\Omega\)
\(tanx=cotx\)
=>\(tanx=tan\left(\dfrac{\Omega}{2}-x\right)\)
=>\(x=\dfrac{\Omega}{2}-x+k\Omega\)
=>\(x=\dfrac{\Omega}{4}+\dfrac{k\Omega}{2}\)
Kết hợp ĐKXĐ, ta được: \(\left[{}\begin{matrix}x=\dfrac{3}{4}\Omega+k2\Omega\\x=\dfrac{7}{4}\Omega+k2\Omega\end{matrix}\right.\)