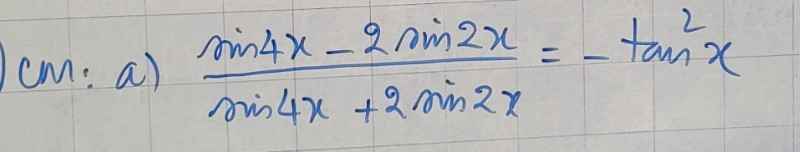\(\dfrac{sin4x-2\cdot sin2x}{sin4x+2\cdot sin2x}\)
\(=\dfrac{2\cdot sin2x\cdot cos2x-2\cdot sin2x}{2\cdot sin2x\cdot cos2x+2\cdot sin2x}\)
\(=\dfrac{2\cdot sin2x\left(cos2x-1\right)}{2\cdot sin2x\left(cos2x+1\right)}=\dfrac{cos2x-1}{cos2x+1}\)
\(=\dfrac{2\cdot cos^2x-1-1}{2\cdot cos^2x-1+1}=\dfrac{2cos^2x-2}{2\cdot cos^2x}=\dfrac{cos^2-1}{cos^2x}\)
\(=\dfrac{-sin^2x}{cos^2x}=-tan^2x\)
Cho hàm số f (x) = 1000 x - 1 + x - 2 x 2 - 1 k h i x > 1 2 a x k h i x ⩽ 1 .Tìm a để hàm số liên tục tại x=1?
A. 3 log 10 2
B. 3 ln 10 2
C. 3 ln 10 + 1 2
D. 3 ln 10 + 1 4
Phương trình sin ( π cos 2 x ) = 1 có nghiệm là:
A. x = kπ, k ∈ Z.
B. π+k2π, k ∈ Z.
C. π/2+kπ, k ∈ Z.
D. ±π/6+kπ, k ∈ Z.
Phương trình sin2x = 1 có nghiệm là:
A. π/2+k4π, k ∈ Z.
B. π/2+kπ, k ∈ Z.
C. π/4+k2π, k ∈ Z.
D. π/4+kπ, k ∈ Z.
Giá trị của A = l i m 2 n 2 + 3 n + 1 3 n 2 - n + 2 bằng:
A. + ∞
B. - ∞
C. 2 3
D. 1
Hàm số y = sin ( π / 2 - x ) + c o t x / 3 là hàm tuần hoàn với chu kì:
A. T = π.
B. T = 2π.
C. T = 3π.
D. T = 6π.
Hàm số y = 2 sin x cos x + cos 2 x có giá trị lớn nhất là
A. 3
B. 2 2
C. 2
D. 2
Cho dãy số (un) xác định bởi u n = n 2 – 4 n – 2 . Khi đó u10 bằng:
A. 48
B. 60
C. 58
D. 10
Mạnh cầm một tờ giấy và lấy kéo cắt thành 7 mảnh sau đó nhặt một trong số bảy mảnh giấy đã cắt và lại cắt thành 7 mảnh. Mạnh cứ tiếp tục cắt như vậy. Sau một hồi, Mạnh thu lại và đếm tất cả các mảnh giấy đã cắt. Hỏi kết quả nào sau đây có thể xảy ra?
A. Mạnh thu được 122 mảnh
B. Mạnh thu được 123 mảnh
C. Mạnh thu được 120 mảnh
D. Mạnh thu được 121 mảnh
Tìm chu kỳ của những hàm số sau đây y=tan(3x+1)
A. π 3
B. 2 π 3
C. 2 π
D. 3 π
