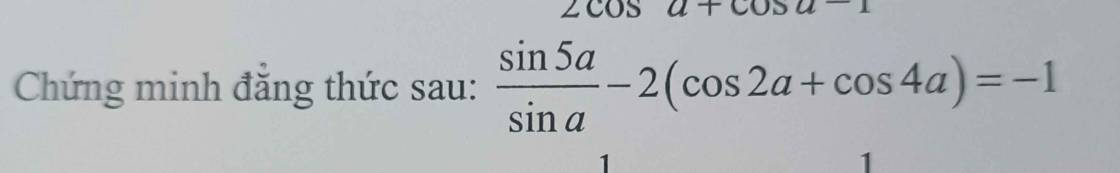Question

    

Answer 1

Lời giải:
\(\frac{\sin 5a}{\sin a}-2(\cos 2a+\cos 4a)=\frac{\sin (a+4a)}{\sin a}-2(\cos 2a+\cos 4a)\\ =\frac{\sin a\cos 4a+\cos a\sin 4a}{\sin a}-2(\cos 2a+\cos 4a)\\ \)

\(=\cos 4a+\frac{2\cos a\sin 2a\cos 2a}{\sin a}-2\cos 2a-2\cos 4a\\ =\cos 4a+\frac{4\cos a\sin a\cos a\cos 2a}{\sin a}-2\cos 2a-2\cos 4a\\ =4\cos ^2a\cos 2a-2\cos 2a-\cos 4a\\ =2\cos 2a(2\cos ^2a-1)-(2\cos ^22a-1)\\ =2\cos 2a\cos 2a-2\cos ^22a+1\\ =2\cos ^22a-2\cos ^22a+1=1\)

Answer 2

Đề sai bạn nhé. Phải bằng 1 chứ không phải -1