Question

Answer 1

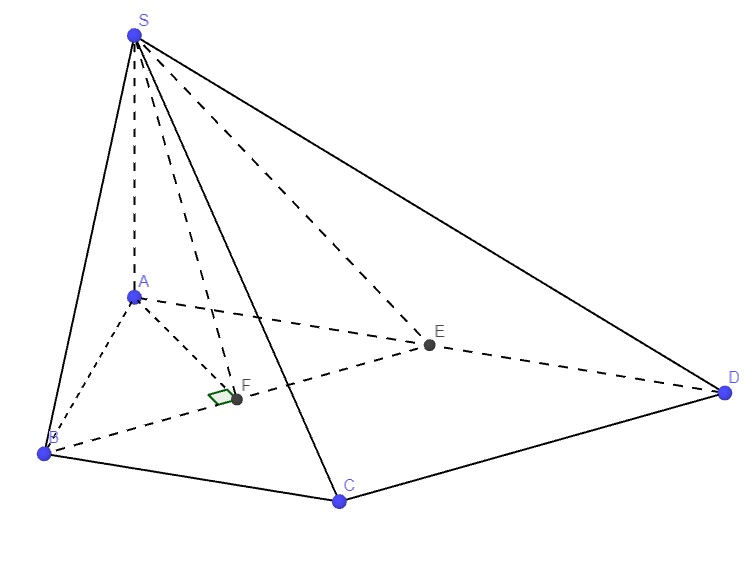
Từ A kẻ \(AF\perp BE\) \(\Rightarrow BE\perp\left(SAF\right)\)

\(\Rightarrow\widehat{SFA}=\left[S,BE,A\right]\)

\(AE=\dfrac{1}{2}AD=a\Rightarrow BE=\sqrt{AB^2+AE^2}=a\sqrt{2}\)

\(AF=\dfrac{AB.AE}{BE}=\dfrac{a\sqrt{2}}{2}\)

\(tan\widehat{SFA}=\dfrac{SA}{AF}=\sqrt{3}\Rightarrow\widehat{SFA}=60^0\)

Answer 2