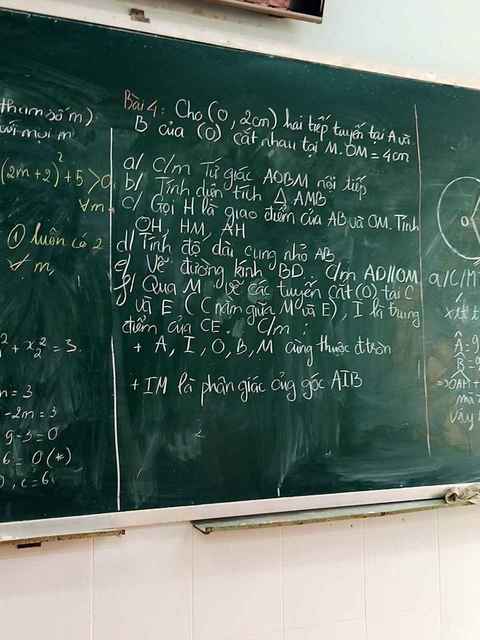a) Xét tứ giác OAMB có
\(\widehat{OAM}\) và \(\widehat{OBM}\) là hai góc đối
\(\widehat{OAM}+\widehat{OBM}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: OAMB là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
b) Xét ΔOAM vuông tại A có
\(\sin\widehat{AOM}=\dfrac{OA}{OM}=\dfrac{2}{4}=\dfrac{1}{2}\)
\(\Leftrightarrow\widehat{AOM}=30^0\)
Xét (O) có
MA là tiếp tuyến có A là tiếp điểm(gt)
MB là tiếp tuyến có B là tiếp điểm(gt)
Do đó: MO là tia phân giác của \(\widehat{AMB}\)(Tính chất hai tiếp tuyến cắt nhau)
Suy ra: \(\widehat{AMB}=2\cdot\widehat{AMO}=2\cdot30^0=60^0\)
Xét (O) có
MA là tiếp tuyến có A là tiếp điểm(gt)
MB là tiếp tuyến có B là tiếp điểm(gt)
Do đó: MA=MB(Tính chất hai tiếp tuyến cắt nhau)
Xét ΔMAB có MA=MB(cmt)
nên ΔMAB cân tại M(Định nghĩa tam giác cân)
Xét ΔMAB cân tại M có \(\widehat{AMB}=60^0\)(cmt)
nên ΔMAB đều(Dấu hiệu nhận biết tam giác đều)
Áp dụng định lí Pytago vào ΔOAM vuông tại A, ta được:
\(OA^2+AM^2=OM^2\)
\(\Leftrightarrow AM^2=OM^2-OA^2=4^2-2^2=12\)
hay \(AM=2\sqrt{3}\left(cm\right)\)
Vì ΔMAB đều nên
\(S_{MAB}=\dfrac{MA^2\cdot\sqrt{3}}{4}=\dfrac{\left(2\sqrt{3}\right)^2\cdot\sqrt{3}}{4}=3\sqrt{3}\left(cm^2\right)\)
c)
Ta có: MA=MB(cmt)
nên M nằm trên đường trung trực của AB(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: OA=OB(=R)
nên O nằm trên đường trung trực của AB(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra OM là đường trung trực của AB
hay OM\(\perp\)AB tại H
Áp dụng hệ thức lượng trong tam giác vuông vào ΔOAM vuông tại A có AH là đường cao ứng với cạnh huyền OM, ta được:
\(OH\cdot OM=OA^2\)
\(\Leftrightarrow OH=\dfrac{OA^2}{OM}=\dfrac{2^2}{4}=1\left(cm\right)\)
Ta có: OH+HM=OM(H nằm giữa O và M)
nên HM=OM-OH=4-1=3(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔOAM vuông tại A có AH là đường cao ứng với cạnh huyền OM, ta được:
\(AH^2=OH\cdot HM\)
\(\Leftrightarrow AH^2=1\cdot3=3\)
hay \(AH=\sqrt{3}\left(cm\right)\)
d) Ta có: OAMB là tứ giác nội tiếp(cmt)
nên \(\widehat{AOB}+\widehat{AMB}=180^0\)(hai góc đối)
\(\Leftrightarrow\widehat{AOB}+60^0=180^0\)
hay \(\widehat{AOB}=120^0\)
\(\Leftrightarrow sđ\stackrel\frown{AB}=120^0\)
e) Xét (O) có
\(\widehat{BAD}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{BAD}=90^0\)(Hệ quả góc nội tiếp)
hay BA\(\perp\)AD
Ta có: BA\(\perp\)AD(cmt)
AB\(\perp\)OM(cmt)
Do đó: AD//OM(Định lí 1 từ vuông góc tới song song)