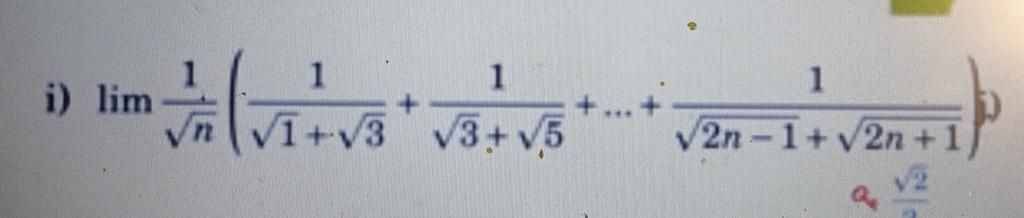\(=lim\dfrac{1}{\sqrt{n}}\left(\dfrac{\sqrt{3}-1}{\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}+...+\dfrac{\sqrt{2n+1}-\sqrt{2n-1}}{\left(\sqrt{2n+1}+\sqrt{2n-1}\right)\left(\sqrt{2n+1}-\sqrt{2n-1}\right)}\right)\)
\(=lim\dfrac{1}{\sqrt{n}}\left(\dfrac{\sqrt{3}-1}{2}+\dfrac{\sqrt{5}-\sqrt{3}}{2}+...+\dfrac{\sqrt{2n+1}-\sqrt{2n-1}}{2}\right)\)
\(=lim\dfrac{1}{\sqrt{n}}\left(\dfrac{\sqrt{2n+1}-1}{2}\right)=lim\left(\dfrac{\sqrt{2n+1}-1}{2\sqrt{n}}\right)\)
\(=lim\left(\dfrac{\sqrt{2+\dfrac{1}{n}}-\dfrac{1}{\sqrt{n}}}{2}\right)=\dfrac{\sqrt{2}}{2}\)
Đúng 2
Bình luận (0)
