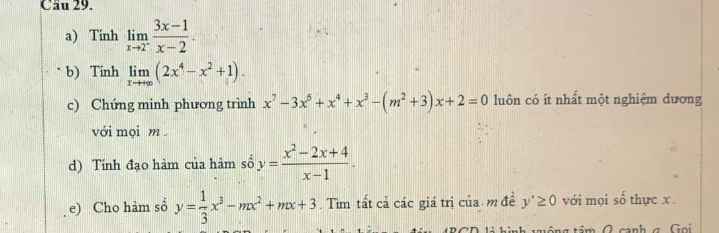a)
\(\lim\limits_{x\to 2+}\frac{3x-1}{x-2}=\lim\limits_{x\to 2+}(3x-1).\frac{1}{x-2}=+\infty\) do $\lim\limits_{x\to 2+}(3x-1)=5>0$ và $\lim\limits_{x\to 2+}\frac{1}{x-2}=+\infty$
b)
$\lim\limits_{x\to \infty+}(2x^4-x^2+1)=\lim\limits_{x\to \infty}[x^4+(x^2-1)^2+x^2]=+\infty$
c)
Đặt $f(x)=x^7-3x^5+x^4+x^3-(m^2+3)x+2$
$f(x)$ liên tục trên $\mathbb{R}$
$f(0)=2>0$
$f(1)=-(m^2+1)<0$ với mọi $m\in\mathbb{R}$
$\Rightarrow f(0)f(1)<0$
Do đó pt $f(x)=0$ luôn có ít nhất 1 nghiệm thuộc $(0;1)$
Tức là pt $f(x)=0$ luôn có ít nhất một nghiệm dương với mọi $m$
d)
\(y=\frac{(x^2-2x+1)+3}{x-1}=\frac{(x-1)^2+3}{x-1}=x-1+\frac{3}{x-1}\)
\(y'=1-\frac{3}{(x-1)^2}\)
e)
$y=\frac{1}{3}x^3-mx^2+mx+3$
$y'=x^2-2mx+m$
Để $y'=x^2-2mx+m\geq 0$ với mọi $x\in\mathbb{R}$ thì:
$\Delta'=m^2-m\leq 0$
$\Leftrightarrow m(m-1)\leq 0$
$\Leftrightarrow 0\leq m\leq 1$
Vậy $m\in [0;1]$