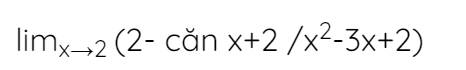\(\lim\limits_{x\rightarrow2}\dfrac{2-\sqrt{x+2}}{x^2-3x+2}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\dfrac{4-x-2}{2+\sqrt{x+2}}}{x^2-3x+2}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{2-x}{2+\sqrt{x+2}}\cdot\dfrac{1}{\left(x-1\right)\left(x-2\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{-1}{\left(x-1\right)\left(2+\sqrt{x+2}\right)}\)
\(=\dfrac{-1}{\left(2-1\right)\left(2+\sqrt{2+2}\right)}=\dfrac{-1}{2+2}=-\dfrac{1}{4}\)
Đúng 1
Bình luận (0)
