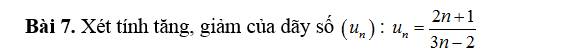Ta có:
\(u_{n+1}=\dfrac{2\left(n+1\right)+1}{3\left(n+1\right)-2}=\dfrac{2n+3}{3n+1}\)
Xét hiệu \(u_{n+1}-u_n\), ta có:
\(u_{n+1}-u_n=\dfrac{2n+3}{3n+1}-\dfrac{2n+1}{3n-2}\)
\(=\dfrac{\left(2n+3\right)\left(3n-2\right)-\left(2n+1\right)\left(3n+1\right)}{\left(3n+1\right)\left(3n-2\right)}\)
\(=\dfrac{\left(6n^2+5n-6\right)-\left(6n^2+5n+1\right)}{\left(3n+1\right)\left(3n-2\right)}\)
\(=\dfrac{-7}{\left(3n+1\right)\left(3n-2\right)}< 0,\forall n\in N\text{*}\)
\(\Rightarrow u_{n+1}< u_n,\forall n\in N\text{*}\)
Vậy dãy số \(\left(u_n\right)\) đã cho là dãy giảm
Đúng 0
Bình luận (0)
