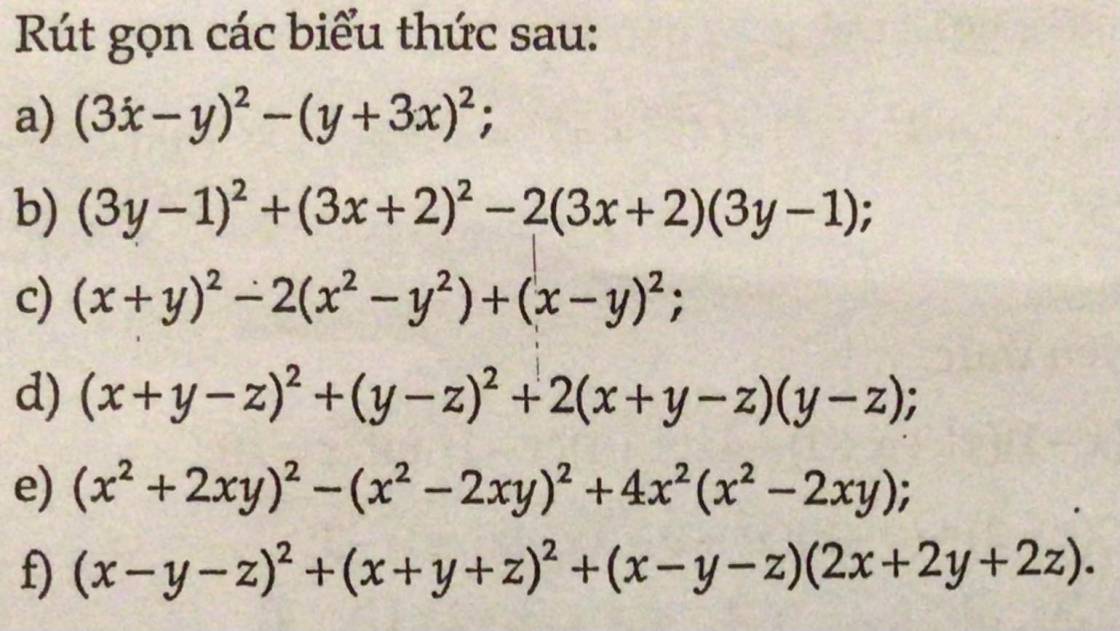a) \(\left(3x-y\right)^2-\left(y+3x\right)^2=\left(3x-y+y+3x\right)\left(3x-y-y-3x\right)\)
\(=6x.\left(-2y\right)=-12xy\)
b) \(\left(3y-1\right)^2+\left(3x+2\right)^2-2\left(3x+2\right)\left(3y-1\right)\)
\(=\left(3y-1-3x-2\right)^2=\left(3y-3x-3\right)^2=9\left(x-y-1\right)^2\)
c) \(\left(x+y\right)^2-2\left(x^2-y^2\right)+\left(x-y\right)^2\)
\(=\left(x+y-x+y\right)^2=4y^2\)
d) \(\left(x+y-z\right)^2+\left(y-z\right)^2+2\left(x+y-z\right)\left(y-z\right)\)
\(=\left(x+y-z+y-z\right)^2=\left(x+2y-2z\right)^2\)
e) \(\left(x^2+2xy\right)^2-\left(x^2-2xy\right)^2+4x^2\left(x^2-2xy\right)\)
\(=\left(x^2+2xy-x^2+2xy\right)\left(x^2+2xy+x^2-2xy\right)+4x^2\left(x^2-2xy\right)\)
\(=8x^3y+4x^2\left(x^2-2xy\right)=4x^2\left(2xy+x^2-2xy\right)=4x^4\)
f) \(\left(x-y-z\right)^2+\left(x+y+z\right)^2+\left(x-y-z\right)\left(2x+2y+2z\right)\)
\(=\left(x-y-z+x+y+z\right)^2=4x^2\)
Lời giải:
a.
$=(3x-y-y-3x)(3x-y+y+3x)=-2y.6x=-12xy$
b.
$=[(3y-1)-(3x+2)]^2=(3y-3x-3)^2=9(y-x-1)^2$
c.
$=(x+y)^2-2(x-y)(x+y)+(x-y)^2=[(x+y)-(x-y)]^2=(2y)^2=4y^2$
d.
$=[(x+y-z)+(y-z)]^2=(x+2y-2z)^2$
e.
$=(x^2+2xy-x^2+2xy)(x^2+2xy+x^2-2xy)+4x^2(x^2-2xy)$
$=4xy.2x^2+4x^2(x^2-2xy)=8x^3y+4x^2(x^2-2xy)$
$=4x^2(2xy+x^2-2xy)=4x^2.x^2=4x^4$
f.
$=(x-y-z)^2+(x+y+z)^2+2(x-y-z)(x+y+z)$
$=[(x-y-z)+(x+y+z)]^2=(2x)^2=4x^2$